In this post we solve the Fibonacci sequence using linear algebra. The Fibonacci equation is a second-order difference equation which is a particular type of sequence.
Sequences
A sequence is a (possibly infinite) set of numbers with a defined order.
\[ a_n = \frac{1}{n}, \textit{ for } n = 0, 1, 2, ..., \]
Difference Equations
A difference equation is a type of sequence. A difference equation expresses the value of the sequence relative to the value of another point in the sequence.
\[ x_{n+1} = 1.5x_n, \textit{ for } n = 0, 1, 2, ..., \]
To evaluate this equation at \(n=3\) we need to know the initial value \(x_0\), and evaluate \(n=1, 2, 3\) in succession. For example, if \(x_0=100\):
\[\begin{align} x_0 & && = 100 \\ x_1 & = 1.5 \times 100 && = 150\\ x_2 & = 1.5 \times 150 && = 225\\ x_3 & = 1.5 \times 225 && = 337.5 \end{align}\]
In the example above, we evaluate the equation recursively. It would be better to be able to evaluate the equation at \(n = 100\) without performing \(100\) calculations. Note that we can also write the equation above in this form:
\[ x_3 = 100 \times 1.5 \times 1.5 \times 1.5 = 337.5 \]
Solving a difference equation means writing the same equation such that it can be evaluated at a given \(n\) without first evaluating \(n=1,2,etc\). The solution to the equation above is:
\[ x_{n} = 1.5^{n} \times x_0, \textit{ for } n = 0, 1, 2, ..., \]
Second Order Difference Equations
The previous example is a first order difference equation because it expresses the value of \(x_n\) as a function of one other sample, \(x_{n-1}\). A second order difference equation is a function of two other samples, for example
\[ x_{n+2} = 1.5x_n + 1.4x_{n+1}, \textit{ for } n = 0, 1, 2, ..., \]
Fibonacci Numbers
The easiest way to describe the Fibonacci sequence is with a second order difference equation. Assume \(F_0 = 0\) and \(F_1 = 1\)
\[ F_{k+2} = F_{k+1} + F_{k} \]
The first eight Fibonacci numbers are:
\[ F_k=0,1,1,2,3,5,8,13,... \]
We can solve the sequence with linear algebra. Let us start our sequence with a vector, \(u_0=\begin{bmatrix}1\\0\end{bmatrix}\). Find the next vector in our sequence, \(u_1\) like this:
\[ u_{1} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \]
More generally:
\[ u_{k+1} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} u_k \]
Note that \(u_0\) contains \(\begin{bmatrix}F_1\\F_0\end{bmatrix}\).
The key to solving the sequence is in the eigenvalues and eigenvectors of \(\begin{bmatrix}1&1\\1&0\end{bmatrix}\). We can write \(u_3\) as
\[ u_3 = \begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix} \begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix} \begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix} \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}3 \\ 2\end{bmatrix} = \begin{bmatrix}F_4 \\ F_3\end{bmatrix} \]
import numpy as np
fib = np.matrix([[1,1],[1,0]])
u_0 = np.matrix([[1],[0]])
fib * fib * fib * u_0 # The * operator is dot product for np.matrix (but not np.array)matrix([[3],
[2]])Eigenvector Solution
The general case of the previous example is:
\[ \begin{align} u_k &= \begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix}^k\begin{bmatrix}1 \\ 0\end{bmatrix}\\ u_k &= A^ku_0 \end{align} \]
We can use eigenvectors and eigenvalues to solve the matrix power (see Eigenvalues and Eigenvectors). First, find the eigenvalues of \(A\):
\[ \begin{align} det\begin{vmatrix} 1 - \lambda & 1\\ 1 & - \lambda \end{vmatrix} & = 0\\ -\lambda(1-\lambda) - 1 & = 0\\ \lambda{}^2 - \lambda - 1 & = 0 \end{align} \]
Solve using the quadratic formula \(\frac{-b \pm \sqrt{b^2-4ac}}{2a} \implies \frac{1 \pm \sqrt{5}}{2} \approx \frac{1 \pm 2.236}{2}\\\), which gives the eigenvalues for our matrix: \[ \begin{align} \lambda_1 & \approx &1.618 \\ \lambda_2 & \approx &-0.618 \end{align} \]
Now we plug our constant eigenvalues (\(\lambda_1\) and \(\lambda_2\)) into \((A-\lambda I)\vec{x}=0\) to find the eigen vectors.
\[ \begin{bmatrix}1-\lambda_1 & 1 \\ 1 & -\lambda_1 \end{bmatrix}\vec{x}_1 = 0 \implies \vec{x}_1 = \begin{bmatrix}\lambda_1 \\ 1\end{bmatrix} \]
Note that this solution is not necessarily intuitive. This is not a valid solution for any arbitrary value of \(\lambda\): our values, \(\lambda_1\) and \(\lambda_2\) are valid solutions. We can use the same process to solve for \(\lambda_2\), revealing eigenvectors \(\begin{bmatrix}\lambda_1 \\1\end{bmatrix}\) and \(\begin{bmatrix}\lambda_2 \\1\end{bmatrix}\). Now create the eigenvector matrix, \(S\) and eigenvalue matrix, \(\Lambda\).
\[ \begin{align} S &= \begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix}\\ \Lambda &= \begin{bmatrix}\lambda_1 & 0 \\ 0 & \lambda_2\end{bmatrix} \end{align} \]
Remeber that \(A^k = S^{-1}\Lambda^kS\). To proceed, invert \(S\). Remember this shortcut for inverting a \(2 \times 2\) matrix.
\[ \begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} =&& \frac{1}{ad-cb} &\begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \\ S^{-1} =&& &\begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix}^{-1} \\ S^{-1} =&& \frac{1}{\lambda_1-\lambda_2} &\begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix}\\ S^{-1} =&& \tfrac{1}{\sqrt{5}} &\begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix} \end{align} \]
Using the components \((A, \Lambda, S, S^{-1},u_0)\):
\[ \begin{align} u_k &= A^ku_0 \\ u_k &= S\Lambda^kS^{-1}u_o \\ u_k &= S\Lambda^k\frac{1}{\sqrt{5}}\begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix}u_0 \\ u_k &= \frac{1}{\sqrt{5}}S\Lambda^k\begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix}u_0 \\ u_k &= \tfrac{1}{\sqrt{5}} \begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix} \begin{bmatrix}\lambda_1 & 0 \\ 0 & \lambda_2\end{bmatrix}^k \begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix} u_0 \\ u_k &= \tfrac{1}{\sqrt{5}} \begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix} \begin{bmatrix}\lambda_1^k & 0 \\ 0 & \lambda_2^k\end{bmatrix} \begin{bmatrix}1 & -\lambda_2\\ -1 & \lambda_1 \end{bmatrix} \begin{bmatrix}1\\0\end{bmatrix} \\ u_k &= \tfrac{1}{\sqrt{5}} \begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix} \begin{bmatrix}\lambda_1^k & 0 \\ 0 & \lambda_2^k\end{bmatrix} \begin{bmatrix}1 \\ -1 \end{bmatrix}\\ u_k &= \tfrac{1}{\sqrt{5}} \begin{bmatrix}\lambda_1 & \lambda_2 \\ 1 & 1\end{bmatrix} \begin{bmatrix}\lambda_1^k \\ -\lambda_2^k\end{bmatrix} \end{align} \]
Verify Solution in Python
import numpy as np
lmbd_1 = (1+np.sqrt(5))/2
lmbd_2 = (1-np.sqrt(5))/2
a = np.matrix([[1, 1], [1, 0]])
s = np.matrix([[lmbd_1, lmbd_2], [1, 1]])
s_inv = np.matrix([[1, -lmbd_2], [-1, lmbd_1]]) * (1/np.sqrt(5))
eig_val = np.matrix([[lmbd_1, 0], [0, lmbd_2]])
u_0 = np.matrix([[1], [0]])
def eig_k(k):
return eig_val ** k
def u_k(k):
return s * eig_k(k) * s_inv * u_0
def fib(n):
f_n = u_k(n)[1,0]
return int(round(f_n))
[fib(n) for n in range(15)][0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]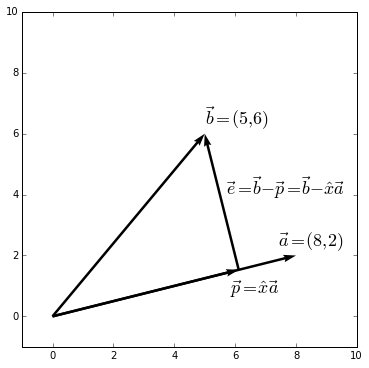
As a simple example we project on to a line. First, calculate