|
|
Image Precision Silhouette Edges
| Ramesh Raskar University of North Carolina at Chapel Hill |
Michael Cohen Microsoft Research |
(Appeared in Symposium on Interactive 3D Graphics (I3DG), Atlanta, April, 1999)
|
|
(
(More
Images ..)
(Download
Demo (SGI or Windows) ) ...........................
(Download Source Code..)
(Paper
in Postscript ..)
(Paper in PDF ..)
(Other Projects ..)
Main Features :
Abstract
Finding and displaying silhouette edges is important in applications ranging from computer vision to nonphotorealistic rendering. To render visible silhouette edges of a polygonal object in a scene from a given viewpoint, we must first find all silhouette edges, i.e. boundaries between adjacent front facing and back-facing surfaces. This is followed by solving the partial visibility problem so that only those parts of silhouette edges, which are not occluded by interior of any front facing surface, are rendered. The scene may optionally be rendered with a lighting model. This paper describes a simple general-purpose method to combine all three operations for any scene composed of objects that can be scan-converted. Using a depth buffer, the rendering process computes the intersection of adjacent front facing and back-facing surfaces in image space at interactive rates. All operations are performed in image-precision and hence special care is taken for the limited numerical precision of the depth buffer. A solution is suggested using view-dependent modification of polygonal objects. The method does not require any preprocessing or adjacency information and hence is applicable for dynamic scenes.
Traditional computer graphics, specifically real-time graphics, usually goes to great lengths to be as photorealistic as possible. However, a simplified diagram is often preferred when an image is required to delineate and explain. Silhouette edges are useful to effectively convey a great deal of information with a very few strokes using nonphotorealistic rendering (NPR). Except [Rossignac92][Markosian97] [Zeleznik96] though, NPR methods have primarily been batch oriented rather than interactive. Most of the techniques are object precision and rely on a-priori information about object models such as the connectivity between surfaces.
Our method assumes that the scene is made up of oriented polygons. To render only visible silhouette edges from a given viewpoint, we must
The visible polygon interiors may optionally be rendered with a lighting model
Our method is based on the observation that only two sets of primitives are needed to compute silhouette edges, the first and second layer of polygons from a given viewpoint. In other words, these include the visible polygons and the layer just behind them which may be either front facing or back facing. Intersection of these two sets gives silhouette edges. In this paper we propose a method specifically for polygonal models but it can be extended to models in any representation for which these two layers or their intersection can be computed. In the proposed method the two nearest layers and their intersection are computed in real time in image precision. The method is robust, general purpose and easy to implement. No pre-processing or adjacency information is required. This allows use of silhouette edges in dynamic scenes, models with changing topology or in models with different levels of detail using traditional polygon rendering pipeline. We also describe how this method can be used to create interesting effects.
Silhouette edges can be rendered using hidden line removal methods [Sutherland74], which are typically batch processes [Dooley90][Elber90]. The method proposed by Markosian et. al. [Markosian97] is real time and works on static polyhedral models with known adjacency information. They use a probabilistic method to identify silhouette edges. The visibility of silhouette edges is computed using modified Appel's hidden-line algorithm [Appel67] assuming the view is generic. The main advantage is that the whole scene does not need to be traversed and hence the silhouette edges of the model can be rendered at a higher frame rate than the model itself. The connectivity information is used to trace out entire silhouette curves by stepping along adjacent silhouette edges. Since the silhouette edges are identified individually, line segments between two vertices can be rendered in expressive styles, for example, in a wobbly, hand-drawn style. Zeleznik's SKETCH system [Zeleznik96] makes use of the polygon-rendering pipeline to highlight edges and boundaries. The method in [Rossignac92] is image precision and does not need adjacency information. The depth-buffer is first updated by rendering the scene in white. Next, after translating backwards, the scene is rendered in thick wireframe mode in black. It does not address the issue of aliasing in the depth-buffer. The work described here is a generalization of the methods outlined in [Rossignac92].

We describe an algorithm to render silhouette edges for polyhedral models in image space. An important observation is that only two sets of polygons are needed to compute visible silhouette edges for a given viewpoint. These two sets are P1, the layer of visible polygons nearest the viewpoint, and P2, the second layer of polygons from that viewpoint. Front facing as well as back-facing polygons are considered in determining these two sets. The intersection of P1 and P2 gives silhouette edges in object space. The first layer of visible polygons can be computed using any visibility algorithm. For a collection of polygonal models of closed objects, this layer is made up of front facing polygons that are completely visible (e.g. front-facing polygons of T1 in Figure 1.b) or visible sub-parts of front facing polygons that are partially visible (e.g. sub-parts of front-facing polygons of T2 in Figure 1.b). The second layer can be computed using the same visibility algorithm as the first after subtracting the polygons in the first layer from the set of all polygons. This second layer, for closed objects, is made up of the back-facing polygons behind the visible surfaces (Figure 1.c). If we assume the viewpoint is not inside any closed object and interiors of polygons do not intersect, the intersection of P1 and P2 gives the desired silhouettes (Figure 1.d).
We can render the silhouette edges by computing the projection of P1, P2 and P1 Ç P2 using a depth buffer (i.e. Z-buffer) directly in image space. The locations where depth values due to P1 and P2 are equal correspond to the projection of the set P1 Ç P2. The following is a pseudo-code to render silhouette edges in black on white background. (When the depth function is f, a pixel with depth d1 overwrites the current pixel in the frame buffer with depth d2, iff f(d1,d2) = true.)
- Draw background with white color
- Enable back face culling, set depth function to ‘Less Than’
- Render (front facing) polygons in white
- Enable front face culling, set depth function ‘Equal To’
- Draw (back-facing) polygons in black
- Repeat for a new viewpoint
This basic method, however, has many limitations. Due to pixel sampling and Z-buffer quantization it is possible that the depth values in the framebuffer due to P1 and P2 may never agree thus pixels closest to the silhouette may be missed. Further, the created silhouette edges will be at most one pixel wide.
The basic method can be slightly modified to render edges of back-facing polygons instead of filled back-facing polygons. Front facing polygons are rendered as before, but back-facing polygons are rendered in wireframe mode and the depth function is 'Less than or Equal'. In [Rossignac92], all the polygons are rendered in wireframe mode after translating them backwards. If desired, the width and color of the edges of any back-facing polygon can be modified according to, say, the distance and orientation with respect to the camera (or the light source), relative importance or size of image. The line segment in the framebuffer is usually rendered with constant thickness and at the same depth value as that of the corresponding polygon edge. This creates visible silhouette edges with constant thickness. This method is very easy to implement and works well when the dihedral angles between adjacent front facing and back-facing polygons are not large. Boundary edges (edges that belong to only one polygon) or any pre-determined edges (such as sharp edges) can be specified separately and rendered along with the edges of back-facing polygons.
As the line width increases, however, one begins to see gaps between silhouette edges made up of neighboring polygons. Because two different types of primitives are involved, polygons and lines, this method also has restrictions when implemented with traditional polygon rendering pipeline.
To increase the area of intersection, we can render front-facing polygons as usual and then render (filled) back-facing polygons pulled slightly forward towards the camera with the depth function set to 'Less than or Equal'. A larger part of the back-facing polygons appear in front of the previously occluding front-facing polygons and this overcomes the problem of numerical precision of the depth buffer. This can be done in the following ways when back-facing polygons are rendered :
If the scaling factor used in translation is sufficiently large, this method creates smooth and continuous silhouette edges. Depending on the dihedral angle between adjacent front facing and back-facing polygons, artistic line drawings with varying line widths are rendered. This looks fine if dihedral angles between adjacent faces are similar e.g. in highly tessellated smooth curved objects. But the width of rendered silhouette edges can become overly large at sharp edges.
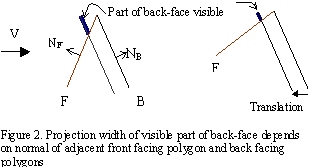
It is easy to see why translation of back-facing polygons will not create uniform line width silhouettes. The width of the resulting silhouette is dependent on the orientation of the back-facing polygon and also the orientation of the corresponding occluding front facing polygon.
If V is the view direction, and for silhouette edge E, NF is the normal of the front facing polygon F and NB is the normal for back-facing polygon B, then the part of B, that will be ‘pushed’ in front of the adjacent front facing polygon, F, is dependent on V·NB and V·NF, as shown in Fig 2.
Depending on taste, the non-uniform width can be considered a feature or a problem. The non-uniform width may provide a pleasing hand drawn appearance, and thus the simple translation approach may be suitable for many applications. On the other hand, if uniform line width is desired, then adjacency information is needed to use the translation methods. This is a requirement we would like to avoid.
Assuming polygons are convex, constant width silhouette edges can be drawn using ‘fat’ back-facing polygons so that the projection of extra area in the image plane is of constant width. The back-facing polygon is fattened by pushing outwards each edge by a distance proportional to z/(V·NB) normal to the edge, where, z is the distance of the midpoint of the edge from the camera.
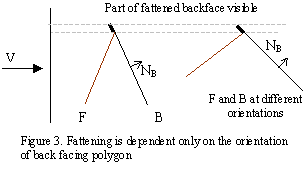
However, the required fattening is also dependent on the orientation of the edges of the back-facing polygon (i.e., fattening is different in different directions for the same polygon). If E is the edge vector so that cos(a) = V·E for a back-facing polygon with normal NB and distance to the camera z, then the required fattening for the edge E is proportional to z*sin(a)/(V·NB) in the direction E ´ NB. (In general, z and V can be approximated and calculated only once for the centroid of the polygon.)
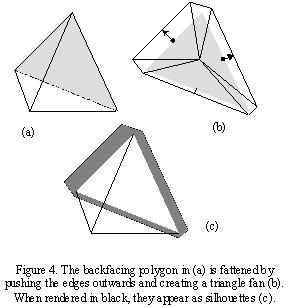
After fattening, an n-sided polygon has 2n vertices connected with the n original edges and small gaps between the split vertices. Completing the fattened polygon involves connecting the shifted vertices and triangulating. The triangulation is achieved by connecting all the new vertices to the midpoint of the polygon. Thus a single polygon is subdivided into 2n triangles in the form of a triangle fan (Figure 4).
To fatten a polygon at run time involves shifting the vertices of the polygon for every new view. Further, the silhouette edge is drawn outside the projection of front facing polygon, instead of on top of existing edges.
This method produces better results than the wireframe method because the rendering involves only polygons. No adjacency information is required. There are no gaps between silhouette edges of neighboring polygons. This method also allows us to use anti-aliasing, transparency and other traditional effects. The silhouette edges can be rendered at different widths using a parameter to control fattening of back-facing triangles. Interesting patterns of silhouette edges can be rendered using texture mapping for back-facing polygons.
The fattening method uses traditional polygon rendering process and can be extended to create many interesting effects. Figure 7 and 8 show a charcoal-like rendering. When the models are finely tessellated, front facing polygons with normal almost perpendicular to the view direction (0 < V·N < 0.1) are also fattened. These fattened parts appear in front of the neighboring front facing polygons creating charcoal-like strokes. The colors are manipulated using a simple lighting method. A gray color I = (1 + V·N)/3 in [0,0.66] is assigned for a vertex with normal N. The nonphotorealistic lighting model suggested by [Gooch98] can also be used for front-facing polygons.
Many applications do not create polygonal models with consistent order of vertices to indicate front-facing or back-facing polygons. In such cases, the polygons in the nearest layer are found by rendering all polygons with a color id and then reading back the framebuffer. Next, all the pixels are set to white without clearing the depth buffer. To render black silhouette edges, it is sufficient to simply render all the remaining polygons in black using any of the methods above. The additional cost of computing the first layer by reading back the framebuffer is dependent only on the size of the framebuffer and independent of scene complexity.
Although, we have focused primarily on rendering visible silhouette edges of polygonal models, the concepts can be extended to other models that can be represented by multiple primitives such as image samples (layered depth images) or analytically defined surfaces for which the two nearest layers can be computed.
We tested the three algorithms on polygonal models with a renderer written in OpenGL running on SGI Indigo2 with MaxImpact. The Venus model shown in Figure 9, 10 and 11 has 5672 triangles. Without silhouette edges, the rendering frame rate was 66 frames/second (fps). When it is rendered with silhouette edges, the frame rates were: for wireframe method 40 fps, z-scaled translation method 50 fps and with view dependent fattening method 11.5 fps. The face model has 13408 triangles. Without silhouette edges, the rendering frame rate was 30 fps. For charcoal-like fattened polygon rendering, the frame rate was 5 fps. For polygon fattening method the reduction of performance factor is large because each back-facing triangle is subdivided into six new triangles. The performance values above include the time to subdivide the triangles.
The auxiliary machine room (amr) model (Figure 5 and 6) has 252,000 triangles. It was rendered at 6 fps using SGI InfiniteReality graphics board. When silhouette edges were rendered using wireframe method, the frame rate drops to 4.2 fps. On an average, a factor of two reduction in performance is noticed. More pictures and image-sequences are available at http://www.cs.unc.edu/~raskar/Sil/
We have described a robust real time technique to render silhouette edges using a traditional polygonal rendering setup. Once a depth buffer has been filled, silhouette edges can be rendered by simply drawing the back-facing polygons in wire-frame mode or by translating the back-facing polygons towards the camera. A more sophisticated method has been described, which allows more flexibility with view-dependent fattening of back-facing edges. None of the methods require pre-processing or adjacency information and hence are ideally suited for dynamic scenes. If the models respond to level-of-detail changes, the silhouette rendering will continue to operate without changes. The method is also robust to inconsistencies in vertex ordering. Shading can also be included with the silhouette rendering to enhance the final look of the model.
There are a few limitations in the silhouette rendering methods discussed. A complete scene traversal is necessary, so all the primitives are processed. The number of back-facing polygons rendered in the case of static models can be reduced by either (a) finding potential silhouette edges using more efficient method such as tracing out silhouette curves [Markosian97] or (b) using normal masks suggested by [Zhang97] to eliminate large number of pairs of polygons that are both front-facing or both back-facing.
As objects move away from the camera, the density of silhouette edges will increase. This may result in a lot of clutter. This can be ameliorated by scaling the fattening according to the average distance of the object from the camera.
The methods outlined above can provide much more meaningful illustrations of complex models than can traditional polygon renderings. The efficiency of the techniques allows them to be seamlessly blended with current methods. This should prove very useful for 3D technical illustration fly-throughs and to create non-photorealistic animations.
Acknowledgements
The authors would like to thank those who provided the geometric models from Hughes Hoppe, Stanford University and Electric Boat. We would also like to thank our colleagues at Microsoft Research, in particular Rick Szeliski and John Snyder for helpful discussions. We thank Matt Cutts for his tremendous help with the video.
References
[Appel67] A. Appel. The notion of quantitative invisibility and the machine rendering of solids. In Proceedings of ACM National Conference, pp.387–393, 1967.
[Dooley90] D. Dooley and M. Cohen. Automatic illustration of 3d geometric models: Lines. In Proceedings of the 1990 Symposium on Interactive 3D Graphics, pp.77–82, March 1990.
[Elber90] G. Elber and E. Cohen. Hidden curve removal for free form surfaces. In Proceedings of SIGGRAPH ’90, pp. 95–104, August 1990.
[Gooch98] Amy Gooch, Bruce Gooch, Peter Shirley, Elaine Cohen. A Non-Photorealistic Lighting Model For Automatic Technical Illustration, Computer Graphics (Proceedings of SIGGRAPH '98), August, 1998.
[Haeberli 90] Paul Haeberli. Paint By Numbers: Abstract Image Representation. In SIGGRAPH 90 Conference Proceedings, August 1990.
[Markosian97] Lee Markosian, Michael A. Kowalski, Samuel J. Trychin, Lubomir D. Bourdev, Daniel Goldstein, and John F. Hughes. Real-Time Nonphotorealistic Rendering, Computer Graphics (Proceedings of SIGGRAPH '97), August, 1997.
[Rossignac92] Jareck Rossignac, Maarten van Emmerik. Hidden Contours on a Framebuffer. Proceedings o fthe 7th Workshop on Computer Graphics Hardware, Eurographics Sept. 1992.
[Saito90] Saito T, Takahashi T, "Comprehensible Rendering of 3-D Shapes," In SIGGRAPH 1990 Conference Proceedings, August 1990.
[Segal92] Mark Segal, Carl Korobkin, Rolf van Widenfelt, Jim Foran, and Paul E. Haeberli. 1992. "Fast Shadows and Lighting Effects using Texture Mapping," In SIGGRAPH 1992 Conference Proceedings, July 1992.
[Siggraph98] Advanced OpenGL Course Notes. http://www.sgi.com/software/opengl/advanced98/notes/node252.html
[Sutherland74] I. Sutherland, R. Sproull, and R. Schumacker. A characterization of ten hidden-surface algorithms. Computing Surveys, 6(1):1–55, March 1974.
[Zeleznik96] R. Zeleznik, K. Herndon, and J. F. Hughes. Sketch: An interface for sketching 3d scenes. In Proceedings of SIGGRAPH ’96, August 1996.
[Zhang97] Hansong Zhang, Kenny Hoff. Fast Backface Culling Using Normal Mask, In Symposium on Interactive 3D Graphics, 1997.