Puzzles from last week
Eight Queens
Put 8 queens on a chess board such that none of them are attacking any of the
others. How many solutions are there?
One solution is:

For each
solution, there are reflective symmetries: left-right; top-bottom;
left-right and top-bottom, and rotational symmetries: clockwise and
counter-clockwise. 
Another group of solutions starts with this
pattern:

What
is the upper bound on the problem?
White Mates in Two
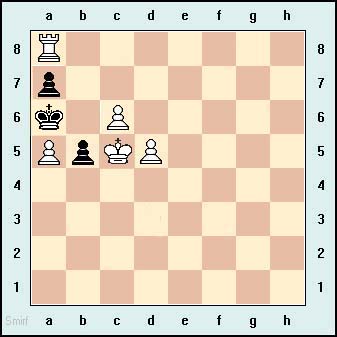
There is no solution unless you think about the most recent move by
Black that led to the current positions. The only move Black could
have made to result in the current board is Black's pawn to B5 en
passant. Thus White's first move is pawn to B6. Black must move A6 to
A5. White moves A8 to A7, capturing the pawn and mate.
Class discussion
Tonight's puzzles mostly deal with being pattern savvy.
Pennies From Heaven (or Hell)
By moving just three coins, make the triangle point down.

By making four slides, where a coin can only slide by rotating
around another until it comes to rest, turn the triangle into a
circle.

Arrange three coins in such a way that by flipping over two coins, three
times, you end up with all three heads up.

By moving just one coin, make two rows of four.

Arrange all five coins so that each one touches every other one.

Move four pennies to make five rows of four

Moving two adjacent pennies at a time, group heads with head and
tails with tails in just three moves, i.e., go from the top row
configuration to the bottom row configuration.

Puzzles for next week
Tiling a Square
How many acute triangles do you need to cover the surface of a square?
It may be easier to consider the problem of tiling an obtuse
triangle.
Desargues Puzzle
This puzzler is inspired by the seventeenth century French engineer and
mathematician, Gerard Desargues.
Using ten coins, make ten rows of three coins each.
Do the same thing with only nine coins.