Tiling a Square, Part 3
How many acute triangles do you need to cover the surface of a square?
It may be easier to consider the problem of tiling an obtuse
triangle. We know that any interior point has to have at least five
line segments connecting it, in order to satisfy the condition that
the angles are all less than 90 degrees. (In other words, it has to be
the interior point of a pentagon where there is a line segment going
to each of the vertices.) We also know that any vertices that are at
angles greater than 90 degrees must have at least one line segment
connected to it. We also know that every point on an edge has to have
at least two line segments connecting it. In the case of an obtuse (or right)
triangle, you need to divide the angle. This suggests the
introduction of a pentagon where one of the vertices is at the vertex
of the obtuse (or right) angle.

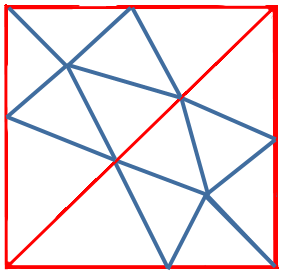
We could use the same reasoning and solve the problem for a square by
starting with two right angles:
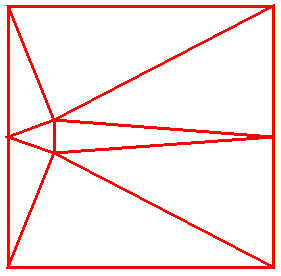
But we can do better still if we start in a corner of the square:
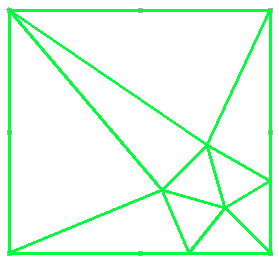
We need at least two interior points, hence two pentagons, but what if they
could overlap?
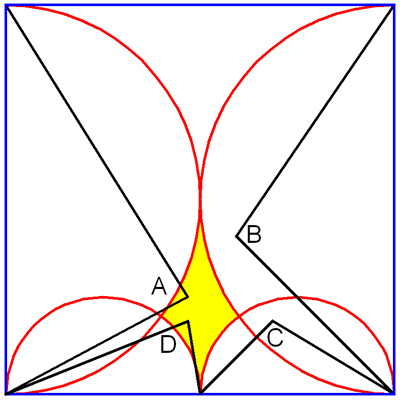
Note that any triangle (A) from the
corners to a point in the yellow region will be acute. Triangles (B)
are obtuse. Likewise, triangles (D) are acute and (C) are
obtuse. (Triangles with a vertex on the circle are right.)
Martin Gardner found a
reference to this puzzle in a 1962 Austrialian Math Journal.
Other solutions:
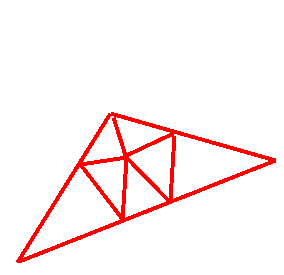
Recursive:
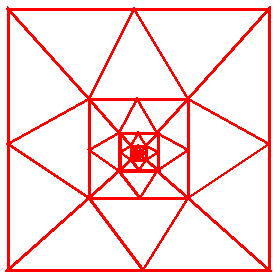
Luis Blackaller's recursive solution:

24:
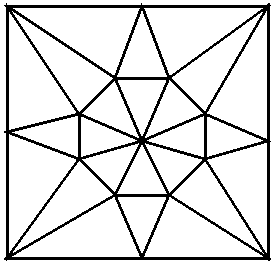
12:
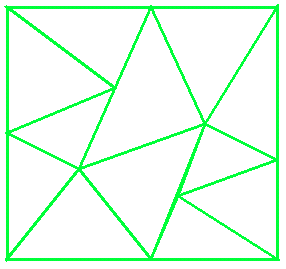
another way of doing just 10:
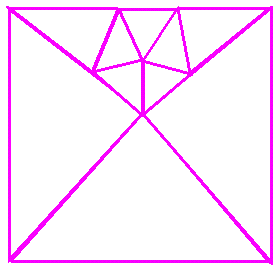
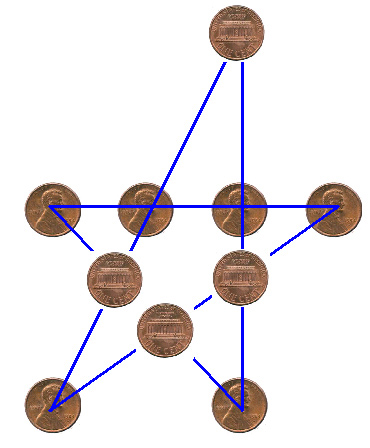
Answer to the triangle to circle puzzle from last week

Answer to the five rows of four puzzle from last week