A Framework for Representing Knowledge
Marvin Minsky
MIT-AI Laboratory Memo 306, June, 1974.
Reprinted in The Psychology of Computer Vision, P. Winston (Ed.), McGraw-Hill, 1975. Shorter versions in J. Haugeland, Ed., Mind Design, MIT Press, 1981, and in Cognitive Science, Collins, Allan and Edward E. Smith (eds.) Morgan-Kaufmann, 1992 ISBN 55860-013-2]
FRAMES
It seems to me that the ingredients of most theories both in Artificial Intelligence and in Psychology have been on the whole too minute, local, and unstructured to account–either practically or phenomenologically–for the effectiveness of common-sense thought. The "chunks" of reasoning, language, memory, and "perception" ought to be larger and more structured; their factual and procedural contents must be more intimately connected in order to explain the apparent power and speed of mental activities.
Similar feelings seem to be emerging in several centers working on theories of intelligence. They take one form in the proposal of Papert and myself (1972) to sub-structure knowledge into "micro-worlds"; another form in the "Problem-spaces" of Newell and Simon (1972); and yet another in new, large structures that theorists like Schank (1974), Abelson (1974), and Norman (1972) assign to linguistic objects. I see all these as moving away from the traditional attempts both by behavioristic psychologists and by logic-oriented students of Artificial Intelligence in trying to represent knowledge as collections of separate, simple fragments.
I try here to bring together several of these issues by pretending to have a unified, coherent theory. The paper raises more questions than it answers, and I have tried to note the theory's deficiencies.
Here is the essence of the theory: When one encounters a new situation (or makes a substantial change in one's view of the present problem) one selects from memory a structure called a Frame. This is a remembered framework to be adapted to fit reality by changing details as necessary.
A frame is a data-structure for representing a stereotyped situation, like being in a certain kind of living room, or going to a child's birthday party. Attached to each frame are several kinds of information. Some of this information is about how to use the frame. Some is about what one can expect to happen next. Some is about what to do if these expectations are not confirmed.
We can think of a frame as a network of nodes and relations. The "top levels" of a frame are fixed, and represent things that are always true about the supposed situation. The lower levels have many terminals–"slots" that must be filled by specific instances or data. Each terminal can specify conditions its assignments must meet. (The assignments themselves are usually smaller "sub-frames.") Simple conditions are specified by markers that might require a terminal assignment to be a person, an object of sufficient value, or a pointer to a sub-frame of a certain type. More complex conditions can specify relations among the things assigned to several terminals.
Collections of related frames are linked together into frame-systems . The effects of important actions are mirrored by transformations between the frames of a system. These are used to make certain kinds of calculations economical, to represent changes of emphasis and attention, and to account for the effectiveness of "imagery."
For visual scene analysis, the different frames of a system describe the scene from different viewpoints, and the transformations between one frame and another represent the effects of moving from place to place. For non-visual kinds of frames, the differences between the frames of a system can represent actions, cause-effect relations, or changes in conceptual viewpoint. Different frames of a system share the same terminals; this is the critical point that makes it possible to coordinate information gathered from different viewpoints.
Much of the phenomenological power of the theory hinges on the inclusion of expectations and other kinds of presumptions. A frame's terminals are normally already filled with "default" assignments. Thus, a frame may contain a great many details whose supposition is not specifically warranted by the situation. These have many uses in representing general information, most likely cases, techniques for bypassing "logic," and ways to make useful generalizations.
The default assignments are attached loosely to their terminals, so that they can be easily displaced by new items that fit better the current situation. They thus can serve also as "variables" or as special cases for "reasoning by example," or as "textbook cases," and often make the use of logical quantifiers unnecessary.
The frame-systems are linked, in turn, by an information retrieval network. When a proposed frame cannot be made to fit reality–when we cannot find terminal assignments that suitably match its terminal marker conditions–this network provides a replacement frame. These inter-frame structures make possible other ways to represent knowledge about facts, analogies, and other information useful in understanding.
Once a frame is proposed to represent a situation, a matching process tries to assign values to each frame's terminals, consistent with the markers at each place. The matching process is partly controlled by information associated with the frame (which includes information about how to deal with surprises) and partly by knowledge about the system's current goals. There are important uses for the information, obtained when a matching process fails. I will discuss how it can be used to select an alternative frame that better suits the situation.
Apology! The schemes proposed herein are incomplete in many respects. First, I often propose representations without specifying the processes that will use them. Sometimes I only describe properties the structures should exhibit. I talk about markers and assignments as though it were obvious how they are attached and linked; it is not.
Besides the technical gaps, I will talk as though unaware of many problems related to "understanding" that really need much deeper analysis. I do not claim that the ideas proposed here are enough for a complete theory, but only that the frame-system scheme may help explain a number of phenomena of human intelligence. The basic frame idea itself is not particularly original–it is in the tradition of the "schema" of Bartlett and the "paradigms" of Kuhn {1970}; the idea of a frame-system is probably more novel. Winograd (1974) discusses the recent trend, in theories of Artificial Intelligence, toward frame-like ideas.
The rest of Part 1 applies the frame-system idea to vision and imagery. In part 2 we turn to linguistic and other kinds of understanding. Part 3 discusses memory, acquisition, and retrieval of knowledge; Part 4 is about control, and Part 5 takes up other problems of vision and spatial imagery.
In the body of the paper I discuss a variety of kinds of reasoning by analogy, and ways to impose stereotypes on reality and jump to conclusions based on partial similarity matching. These are basically uncertain methods. Why not use methods that are more "logical" and certain? Section 6 is a sort of Appendix which argues that traditional logic cannot deal very well with realistic, complicated problems because it is poorly suited to represent approximations to solutions–and these are absolutely vital.
Thinking always begins with suggestive but imperfect plans and images; these are progressively replaced by better–but usually still imperfect–ideas.
"For there exists a great chasm between those, on the one side, who relate everything to a single central vision, one system more or less coherent or articulate, in terms of which they understand, think and feel–a single, universal, organizing principle in terms of which alone all that they are and say has significance–and, on the other side, those who pursue many ends, often unrelated and even contradictory, connected, if at all, only in some de facto way, for some psychological or physiological cause, related by no moral or esthetic principle."–Isaiah Berlin {The Hedgehog and the Fox}.
When we enter a room we seem to see the entire scene at a glance. But seeing is really an extended process. It takes time to fill in details, collect evidence, make conjectures, test, deduce, and interpret in ways that depend on our knowledge, expectations and goals. Wrong first impressions have to be revised. Nevertheless, all this proceeds so quickly and smoothly that it seems to demand a special explanation.
Some people dislike theories of vision that explain scene-analysis largely in terms of discrete, serial, symbolic processes. They feel that although programs built on such theories may indeed seem to "see," they must be too slow and clumsy for a nervous system to use. But the alternative usually proposed is some extreme position of "holism" that never materializes into a technical proposal. I will argue that serial symbolic mechanisms could indeed explain much of the apparent instantaneity and completeness of visual experience.
Some early Gestalt theorists tried to explain a variety of visual phenomena in terms of global properties of electrical fields in the brain. This idea did not come to much (Koffka, 1935). Its modern counterpart, a scattered collection of attempts to use ideas about integral transforms, holograms, and interference phenomena, has done no better. In spite of this, most thinkers outside (and some inside) the symbolic processing community still believe that only through some sort of field-like global parallel process could the required speed be attained.
While my theory is thus addressed to basic problems of Gestalt psychology, the method is fundamentally different. In both approaches, one wants to explain the structuring of . sensory data into wholes and parts. Gestalt theorists hoped this could be based primarily on the operation of a few general and powerful principles; but these never crystallized effectively and the proposal lost popularity. In my theory the analysis is based on many interactions between sensations and a huge network of learned symbolic information. While ultimately those interactions must themselves be based also on a reasonable set of powerful principles, the performance theory is separate from the theory of how the system might originate and develop.
1.2 PARALLELISM
Would parallel processing help? This is a more technical question than it might seem. At the level of detecting elementary visual features, texture elements, stereoscopic and motion-parallax cues, it is obvious that parallel processing might be useful. At the level of grouping features into objects, it is harder to see exactly how to use parallelism, but one can at least conceive of the aggregation of connected "nuclei" (Guzman, 1968), or the application of boundary line constraint semantics (Waltz, 1972), performed in a special parallel network.
At "higher" levels of cognitive processing, however, I suspect fundamental limitations in the usefulness of parallelism. Many "integral" schemes were proposed in the literature on "pattern recognition" for parallel operations on pictorial material–perceptrons, integral transforms, skeletonizers, and so forth. These mathematically and computationally interesting schemes might quite possibly serve as ingredients of perceptual processing theories. But as ingredients only! Basically, "integral" methods work only on isolated figures in two dimensions. They fail disastrously to cope with complicated, three-dimensional scenery. Why?
In complex scenes, the features belonging to different objects have to be correctly segregated to be meaningful; but solving this problem–which is equivalent to the traditional Gestalt "figure-ground" problem–presupposes solutions for so many visual problems that the possibility and perhaps even the desirability of a separate recognition technique falls into question, as noted by Minsky and Papert (1969). In three dimensions the problem is further confounded by the distortion of perspective and by the occlusions of parts of each figure by its own surfaces and those of other figures.
The new, more successful symbolic theories use hypothesis formation and confirmation methods that seem, on the surface at least, more inherently serial. It is hard to solve any very complicated problem without giving essentially full attention, at different times, to different sub-problems. Fortunately, however, beyond the brute idea of doing many things in parallel, one can imagine a more serial process that deals with large, complex, symbolic structures as units! This opens a new theoretical "niche" for performing a rapid selection of large substructures; in this niche our theory hopes to find the secret of speed, both in vision and in ordinary thinking.
1.3 ARTIFICIAL INTELLIGENCE AND HUMAN PROBLEM SOLVING .
In this essay I draw no boundary between a theory of human thinking and a scheme for making an intelligent machine; no purpose would be served by separating these today since neither domain has theories good enough to explain–or to produce–enough mental capacity. There is, however, a difference in professional attitudes. Workers from psychology inherit stronger desires to minimize the variety of assumed mechanisms. I believe this leads to attempts to extract more performance from fewer "basic mechanisms" than is reasonable. Such theories especially neglect mechanisms of procedure control and explicit representations of processes. On the other side, workers in Artificial Intelligence have perhaps focused too sharply on just such questions. Neither have they given enough attention to the structure of knowledge, especially procedural knowledge.
It is understandable why psychologists are uncomfortable with complex proposals not based on well established mechanisms. But I believe that parsimony is still inappropriate at this stage, valuable as it may be in later phases of every science. There is room in the anatomy and genetics of the brain for much more mechanism than anyone today is prepared to propose, and we should concentrate for a while more on sufficiency efficiency than on necessity.
Up to a few years ago, the primary goal of AI work on vision had to be sufficiency: to find any way at all to make a machine analyze scenes. Only recently have we seen the first signs of adequate capacity to aggregate features and cues correctly into parts and wholes. I cite especially the sequence of work of Roberts (1965), Guzman (1968), Winston (1970), Huffman (1971), Clowes (1971), Shirai (1972), Waltz (1972), Binford (1971), Nevatia (1973) and Agin (1973) to indicate some steps toward adequate analyses of figure-ground, whole-part, and group-structuring issues.
Although this line of development is still primitive, I feel it is sound enough that we can ask it to explain not only the brute performance of vision but also some of its speed and smoothness. Some new issues confront our theory when we turn from sufficiency to efficiency: How can different kinds of "cues" lead so quickly to identifying and describing complex situations? How can one make changes in case of error or if new evidence is found? How does one resolve inconsistencies? How can position change without recomputing everything? What about moving objects? How does the vision process exploit knowledge associated with general, non-visual activities? How does one synthesize the information obtained from different viewpoints? How can the system exploit generally correct expectations about effects of contemplated actions. Can the theory account for the phenomenological effects of imagery, the self-directed construction and manipulation of imaginary scenes?
Very little was learned about such matters in the main traditions of behavioral or of perceptual psychology; but the speculations of some earlier psychologists, particularly of Bartlett (1932), have surely found their way into this essay. In the more recent tradition of symbolic information processing theories, papers like those of Newell (1973) and Pylyshyn (1973) take larger technical steps to formulate these issues.
1.4 TRACKING THE IMAGE OF A CUBE .
"But in the common way of taking the view of any opake object, that part of its surface, which fronts the eye, is apt to occupy the mind alone, and the opposite, nay even every other part of it whatever, is left unthought of at that time: and the least motion we make to reconnoitre any other side of the object, confounds our first idea, for want of the connexion of the two ideas, which the complete knowledge of the whole world would naturally have given us, if we had considered it the other way before." –W. Hogarth {The Analysis of Beauty . .
I begin by developing a simplified frame-system to represent the perspective appearances of a cube. Later I will adapt it to represent the insides of rooms and to acquiring, using, and revising the kinds of information one needs to move around within a house.
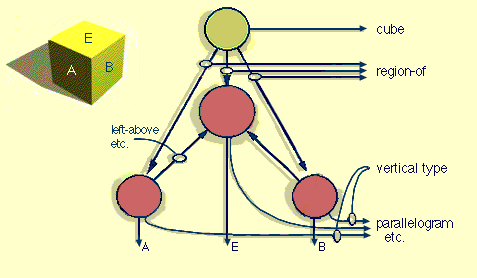
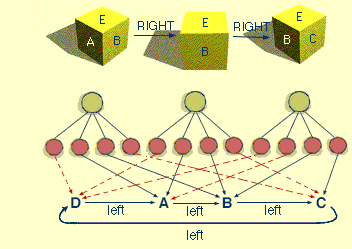
In the tradition of Guzman and Winston, we assume that the result of looking at a cube is a structure something like that in figure 1.1.

The substructures "A" and "B" represent details or decorations on two faces of the cube. When we move to the right, face "A" disappears from view, while the new face decorated with "C" is now seen. If we had to reanalyse the scene from the start, we would have to
(1) lose the knowledge about "A,"
(2) recompute "B," and
(3) compute the description of "C."
But since we know we moved to the right, we can save "B" by assigning it also to the "left face" terminal of a second cube-frame. To save "A" (just in case!) we connect it also to an extra, invisible face-terminal of the new cube-schema as in figure 1.2.
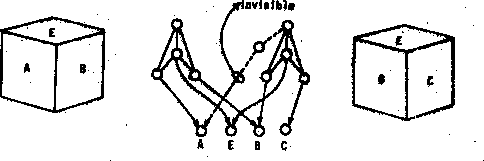
If later we move back to the left, we can reconstruct the first scene without any perceptual computation at all: . just restore the top-level pointers to the first cube-frame. We now need a place to store "C"; we can add yet another invisible face to the right in the first cube-frame! See figure 1.3.
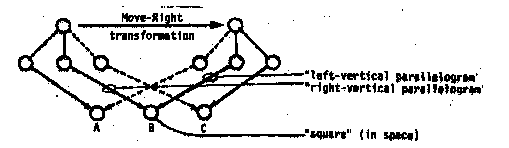
We could extend this to represent further excursions around the object. This would lead to a more comprehensive frame system, in which each frame represents a different "perspective" of a cube. In figure 1.4 there are three frames corresponding to 45-degree MOVE-RIGHT and MOVE-LEFT actions.
If we pursue this analysis, the resulting system can become very large; more complex objects need even more different projections. It is not obvious either that all of them are normally necessary or that just one of each variety is adequate. It all depends.
I am not proposing that this kind of complicated structure is recreated every time one examines an object. I imagine instead that a great collection of frame systems is stored in permanent memory, and one of them is evoked when evidence and expectation make it plausible that the scene in view will fit it. How are they acquired? I will propose that if a chosen frame does not fit well enough, and if no better one is easily found, and if the matter is important enough, then an adaptation of the best one so far discovered will be constructed and remembered for future use.
Do we build such a system for every object we know? That would seem extravagant. More likely, I would think, one has special systems for important objects but also a variety of frames for generally useful "basic shapes"; these are composed to form frames for new cases.
The different frames of a system resemble the multiple "models" described in Guzman (1967) and Winston (1970). Different frames correspond to different views, and the names of pointers between frames correspond to the motions or actions that change the viewpoint. Later I discuss whether these views should be considered as two- or as three-dimensional.
Each frame has terminals for attaching pointers to substructures. Different frames can share the same terminal, which can thus correspond to the same physical feature as seen in different views. This permits us to represent, in a single place, view independent information gathered at different times and places. This is important also in non-visual applications.
The matching process which decides whether a proposed frame is suitable is controlled partly by one's current goals and partly by information attached to the frame; the frames carry terminal markers and other constraints, while the goals are used to decide which of these constraints are currently relevant. Generally, the matching process could have these components:
(1) A frame, once evoked on the basis of partial evidence or expectation, would first direct a test to confirm its own appropriateness, using knowledge about recently noticed features, loci, relations, and plausible subframes. The current goal list is used to decide which terminals and conditions must be made to match reality.
(2) Next it would request information needed to assign values to those terminals that cannot retain their default assignments. For example, it might request a description of face "C," if this terminal is currently unassigned, but only if it is not marked "invisible." Such assignments must agree with the current markers at the terminal. Thus, face "C" might already have markers for such constraints or expectations as:
* Right-middle visual field.
* Must be assigned.
* Should be visible; if not, consider moving right.
* Should be a cube-face subframe.
* Share left vertical boundary terminal with face "B."
* If failure, consider box-lying-on-side frame.
* Same background color as face "B."
(3) Finally, if informed about a transformation (e.g., an impending motion) it would transfer control to the appropriate other frame of that system.
Within the details of the control scheme are opportunities to embed many kinds of knowledge. When a terminal-assigning attempt fails, the resulting error message can be used to propose a second-guess alternative. Later I will suggest using these to organize memory into a Similarity Network as proposed in Winston (1970).
1.5 IS VISION SYMBOLIC?
Can one really believe that a person's appreciation of three-dimensional structure can be so fragmentary and atomic as to be representable in terms of the relations between parts of two-dimensional views? Let us separate, at once, the two issues: is imagery symbolic and is it based on two-dimensional fragments? The first problem is one of degree; surely everyone would agree that at some level vision is essentially symbolic. The quarrel would be between certain naive conceptions on one side–in which one accepts seeing either as picture-like or as evoking imaginary solids–against the confrontation of such experimental results of Piaget (1956) and others in which many limitations that one might fear would result from symbolic representations are shown actually to exist!
Thus we know that in the art of children (and, in fact, in that of most adult cultures) graphic representations are indeed composed from very limited, highly symbolic ingredients. See, for example, chapter 2 of Gombrich (1969). Perspectives and occlusions are usually not represented "realistically" but by conventions. Metrical relations are grossly distorted; complex forms are replaced by signs for a few of their important features. Naive observers do not usually recognize these devices and maintain that they do "see and manipulate pictorial images" in ways that, to them, could not conceivably be accounted for by discrete descriptions.
As for our second question: the issue of two- vs. three-dimensions evaporates at the symbolic level. The very concept of dimension becomes inappropriate. Each type of symbolic representation of an object serves some goals well and others poorly. If we attach the relation labels left of, right of, and above between parts of the structure, say, as markers on pairs} of terminals, certain manipulations will work out smoothly; for example, some properties of these relations are "invariant" if we rotate the cube while keeping the same face on the table. Most objects have "permanent" tops and bottoms. But if we turn the cube on its side such predictions become harder to make; people have great difficulty keeping track of the faces of a six-colored cube if one makes them roll it around in their mind.
If one uses instead more "intrinsic" relations like next to and opposite to, then turning the object on its side disturbs the "image" much less. In Winston we see how systematic replacements (e.g., of "left" for "behind," and "right" for "in-front-of") can simulate the effect of spatial rotation.
Hogarth (1753) did not take a position on the symbolic issue, but he did consider good imagery to be an acquired skill and scolds artists who give too little time to perfecting the ideas they ought to have in their minds of the objects in nature. He recommends that
"… he who will undertake the acquisition of perfect ideas of the distances, bearings, and oppositions of several material points and lines in even the most irregular figures, will gradually arrive at the knack of recalling them into his mind when the objects themselves are not before him–and will be of infinite service to those who invent and draw from fancy, as well as to enable those to be more correct who draw from the life."
Thus, deliberate self-discipline in cataloguing relations between points on opposing surfaces is, he thinks, a key to understanding the invariant relations between the visible and invisible parts; they supply the information needed to imagine oneself within the interior of the object, or at other unexperienced locations; he thus rejects the naive image idea.
Some people believe that we solve spatial problems by maintaining in one's head, somehow, the analog of a three-dimensional structure. But even if one somehow could assemble such a model there would remain, for the "mind's eye," most of the old problems we had for the real eye as well as the new and very hard problem of assembling–from two-dimensional data–the hypothetical imaginary solid.
Although these arguments may seem to favor interconnected two-dimensional views for aggregation and recognition, I do not consider these satisfactory for planning or for manipulative activities. Another representation, still symbolic but in terms of basic solid forms, would seem more natural. Thus a telephone handset could be described in terms of two modified spherical forms connected by a curved, rectangular bar. The problem of connecting two or more qualitatively different ways to represent the same thing is discussed, but not solved, in a later section.
1.6 SEEING A ROOM
Visual experience seems continuous. One reason is that we move continuously. A deeper explanation is that our "expectations" usually interact smoothly with our perceptions. Suppose you were to leave a room, close the door, turn to reopen it, and find an entirely different room. You would be shocked. The sense of change would be hardly less striking if the world suddenly changed before your eyes.
A naive theory of phenomenological continuity is that we see so quickly that our image changes as fast as does the scene. Below I press an alternative theory: the changes in one's frame-structure representation proceed at their own pace; the system prefers to make small changes whenever possible; and the illusion of continuity is due to the persistence of assignments to terminals common to the different view-frames. Thus, continuity depends on the confirmation of expectations which in turn depends on rapid access to remembered knowledge about the visual world.
Just before you enter a room, you usually know enough to "expect" a room rather than, say, a landscape. You can usually tell just by the character of the door. And you can often select in advance a frame for the new room. Very often, one expects a certain particular room. Then many assignments are already filled in.
The simplest sort of room-frame candidate is like the inside of a box. Following our cube-model, the room-frame might have the top-level structure shown in figure 1.5.
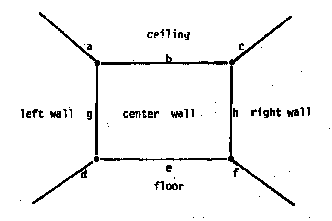
One has to assign to the frame's terminals the things that are seen. If the room is familiar, some are already assigned. If no expectations are recorded already, the first priority might be locating the principal geometric landmarks.
To fill in LEFT WALL one might first try to find edges "a" and "d" and then the associated corners "ag" and "gd." Edge "g," for example, is usually easy to find because it should intersect any eye-level horizontal scan from left to right. Eventually, "ag," "gb," and "ba" must not be too inconsistent with one another–because they are the same physical vertex.
However the process is directed, there are some generally useful knowledge-based tactics. It is probably easier to find edge "e" than any other edge, because if we have just entered a normal rectangular room, then we may expect that
Edge "e" is a horizontal line.
It is below eye level.
It defines a floor-wall texture boundary.
Given an expectation about the size of a room, we can estimate the elevation of "e," and vice versa. In outdoor scenes, "e" is the horizon and on flat ground we can expect to see it at eye-level. If we fail quickly to locate and assign this horizon, we must consider rejecting the proposed frame: either the room is not normal or there is a large obstruction.
The room-analysis strategy might try next to establish some other landmarks. Given "e," we next look for its left and right corners, and then for the verticals rising from them. Once such gross geometrical landmarks are located, we can guess the room's general shape and size. This might lead to selecting a new frame better matched to that shape and size, with additional markers confirming the choice and completing the structure with further details.
Of course a competent vision system has to analyze the scene not merely as a picture, but also in relation to some sort of external space-frame. For vision to proceed smoothly when one is moving around, one has to know where each feature "is," in the external world of mobility, to compensate for transformations induced by eye, head, and body motions, as well as for gross locomotion.
1.7 SCENE ANALYSIS AND SUBFRAMES
If the new room is unfamiliar, no pre-assembled frame can supply fine details; more scene-analysis is needed. Even so, the complexity of the work can be reduced, given suitable subframes for constructing hypotheses about substructures in the scene. How useful these will be depends both on their inherent adequacy and on the quality of the expectation process that selects which one to use next. One can say a lot even about an unfamiliar room. Most rooms are like boxes, and they can be categorized into types: kitchen, hall, living room, theater, and so on. One knows dozens of kinds of rooms and hundreds of particular rooms; one no doubt has them structured into some sort of similarity network for effective access. See §3.4.
A typical room-frame has three or four visible walls, each perhaps of a different "kind." One knows many kinds of walls: walls with windows, shelves, pictures, and fireplaces. Each kind of room has its own kinds of walls. A typical wall might have a 3 x 3 array of region-terminals (left-center-right) x (top-middle-bottom) so that wall-objects can be assigned qualitative locations. One would further want to locate objects relative to geometric inter-relations in order to represent such facts as "Y is a little above the center of the line between X and Z."
In three dimensions, the location of a visual feature of a subframe is ambiguous, given only eye-direction. A feature in the middle of the visual field could belong either to a Center Front Wall object or to a High Middle Floor object; these attach to different subframes. The decision could depend on reasoned evidence for support, on more directly visual distance information derived from stereo disparity or motion-parallax, or on plausibility information derived from other frames: a clock would be plausible only on the wall-frame while a person is almost certainly standing on the floor.
I do not imagine the boundaries of spatial frame-cells to be constrained by accurate metrical dimensions. Each cell terminal would specify the (approximate) location of a typically central place in that cell, and some comparative size range. We expect correct topological constraints; a left-wall-edge must agree to stay to the left of any object assigned to lie flat against that wall. The process of "matching" a scene against all such constraints may result in a degree of "strain," as a cell expands (against its size-range specification) to include objects proposed for its interior. Tolerance of such strains should depend on one's current purpose and past experience. While this might seem complicated, I do not think that the richness of visual experience supports a drive for much simpler theories.
1.8 PERSPECTIVE AND VIEWPOINT TRANSFORMATIONS
In sum, at Substage IIIB (age 8 or 9, typically) the operations required to coordinate perspectives are complete, and in the following quite independent forms. First, to each position of the observer there corresponds a particular set of left-right, before-behind relations between the objects... These are governed by the projections and sections appropriate to the visual plane of the observer (perspective). During this final substage the point to point nature of the correspondence between position and perspective is discovered.
Second, between each perspective viewpoint valid for a given position of the observer and each of the others, there is also a correspondence expressed by specific changes of left-right, before-behind relations, and consequently by changes of the appropriate projections and sections. It is this correspondence between all possible points of view which constitutes co-ordination of perspectives... though as yet only in a rudimentary form."–Jean Piaget and Barbel Inhelder, in {The Child's Conception of Space}
When we move about a room, the shapes of things change. How can these changes be anticipated, or compensated, without complete reprocessing? The results of eye and head rotation are simple: things move in the visual field but keep their shapes; but changing place causes large shape changes that depend both on angle and on distance relations between the object and observer. The problem is particularly important for fast-moving animals because a model of the scene must be built up from different, partially analyzed views. Perhaps the need to do this, even in a relatively primitive fashion, was a major evolutionary stimulus to develop frame-systems, and later, other symbolic mechanisms.
Given a box-shaped room, lateral motions induce orderly changes in the quadrilateral shapes of the walls.
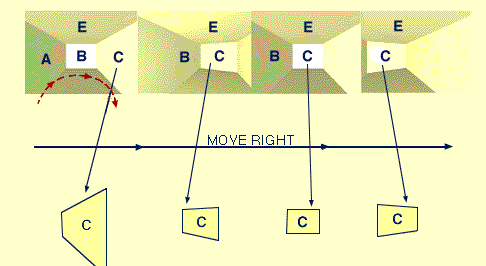
A picture-frame rectangle, lying flat against a wall, should transform in the same way as does its wall. If a "center-rectangle" is drawn on a left wall it will appear to project out because one makes the default assumption that any such quadrilateral is actually a rectangle hence must lie in a plane that would so project. In figure 1.7A, both quadrilaterals could "look like" rectangles, but the one to the right does not match the markers for a "left rectangle" subframe (these require, e.g., that the left side be longer than the right side). That rectangle is therefore represented by a center-rectangle frame, and seems to project out as though parallel to the center wall.
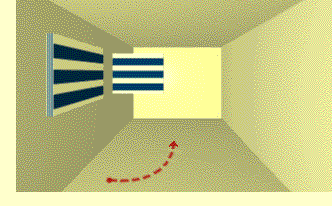
Thus we must not simply assign the label "rectangle" to a quadrilateral but to a particular frame of a rectangle-system. When we move, we expect whatever space-transformation is applied to the top-level system will be applied also to its subsystems as suggested in figure 1.7B. Similarly the sequence of elliptical projections of a circle contains congruent pairs that are visually ambiguous as shown in figure 1.8.
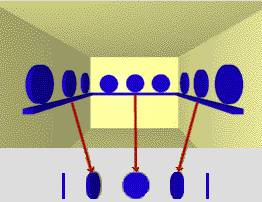
But because wall objects usually lie flat, we assume that an ellipse on a left wall is a left-ellipse, expect it to transform the same way as the left wall, and are surprised if the prediction is not confirmed.
Is it plausible that a finite, qualitative symbolic system can represent perspective transformations adequately? People in our culture are chronically unrealistic about their visualization abilities, e.g., to visualize how spatial relations will appear from other viewpoints. We noted that people who claim to have clear images of such configurations often make qualitative errors in describing the rotations of a simple multicolored cube. And even where we are actually able to make accurate metrical judgements we do not always make them; few people are disturbed by Huffman's (1970) "impossible" pyramid:
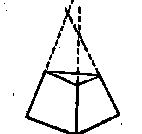
This is not a perspective of any actual truncated pyramid; if it were the three edges, when extended, would all meet at one point. In well-developed skills, no doubt, people can routinely make more precise judgements, but this need not require a different mechanism. Where a layman uses 10 frames for some job, an expert might use 1000 and thus get the appearance of a different order of performance.
In any case, to correctly anticipate perspective changes in our systems, the top-level transformation must induce appropriate transforms in the subframe systems. To a first approximation, this can be done simply by using the same transformation names. Then a "move-right" action on a room frame would induce a "move-right" action on objects attached to the wall subframes (and to their subframes).
I said "first approximation" because this scheme has a serious bug. If you stand near a left wall and walk forward, the nearby left-wall objects suffer a large "move-right" transform, the front wall experiences a "move closer" transform, and the right wall experiences a small "move left" transform. So matters are not so simple that it is always sufficient merely to transmit the motion name down to lower levels.
1.9 OCCLUSIONS
When we move to the right, a large object in the center foreground will probably occlude any further-away object to its visual left. When motion is planned, one should be able to anticipate some of these changes. Some objects should become invisible and other objects should appear. Our prototype cube-system has no occlusion problem because the scene is completely convex; the disappearance of an entire side and its contents is easily handled at the top level. But in a room, which is basically concave, the sub-objects of different terminals can occlude one another. We consider two extreme strategies:
LOCAL ASSEMBLIES: Just as for the different views of a single object, occlusions of a familiar assembly could be handled by a special frame system for that configuration; for example, a chair and table as in figure 1.10. If we apply the same perspective transformations to such a "niche-frame" that we apply to its superiors, then to a first approximation, occlusions between the objects are handled automatically.
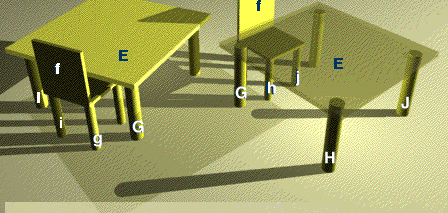
This works for compact, familiar subgroups of objects but cannot handle the details of occlusions between elements of the niche and other things in the room. For engineering applications the scheme's simplicity would not outweigh its frequent errors. As a theory of human performance, it might be good enough. A trained artist or draftsman can answer such questions better, but such activities proceed slowly and need not be explained by a first-order theory concerned mainly with speed.
A more radical scheme would make all perspective frames subsidiary to a central, common, space-frame system. The terminals of that system would correspond to cells of a gross subjective space, whose transformations represent, once-and-for-all, facts about which cells occlude others from different viewpoints.
If there were such a supersystem, would it be learned or innate? The context of the Piaget-Inhelder quotation presents evidence that complete coordination structures of this sort are not available to children in their first decade.
IMAGERY AND FRAME SYSTEMS
"Everyone will readily allow that there is a considerable difference between the perceptions of the mind, when a man feels the pain of excessive heat, or the pleasure of moderate warmth, and when he afterwards recalls to his memory this sensation, or anticipates it by his imagination. These faculties may mimic or copy the perceptions of the senses; but they never can entirely reach the force and vivacity of the original sentiment.... The most lively thought is still inferior to the dullest sensation."– D. Hume {Enquiry into Human Understanding}
A theory of seeing should also be a theory of imagining.
For in our view both have the same end results: assignments to terminals of frames. Everyone will agree with Hume that there are differences between vision and imagery. Hume theorizes that this is because vision is immediate and direct, whereas imagery is derived from recombinations of memories of direct "impressions" and that some of the force is lost, somehow, in the storage, retrieval, and computation. I propose instead that
Seeing seems more vivid than Imagining because its assignments are less flexible; they more firmly resist the attempts of other processes to modify them.
If you try to change the description of a scene actually projected on your retinas, your vision system is likely simply to change it right back. There is no correspondingly rigid constraint on fantasies.
However, even "seen" assignments are not completely inflexible; anyone can learn to mentally reverse the interpretation of a skeleton-cube drawing. So-called "ambiguous" figures are those that are easy to describe in different ways. Changing a frame for such a purpose amounts to a change in "descriptive viewpoint," one in which the action or transformation is symbolic rather than physical; in any case, we are told that there are mental states in which fantasies are more inflexible than "direct impressions" and even, sometimes, more "vivid."
1.11 DEFAULT ASSIGNMENTS
While both Seeing and Imagining result in assignments to frame terminals, Imagination leaves us wider choices of detail and variety of such assignments. I conjecture that frames are never stored in long-term memory with unassigned terminal values. Instead, what really happens is that frames are stored with weakly-bound default assignments at every terminal! These manifest themselves as often-useful but sometimes counter-productive stereotypes.
Thus if I say, "John kicked the ball," you probably cannot think of a purely abstract ball, but must imagine characteristics of a vaguely particular ball; it probably has a certain default size, default color, default weight. Perhaps it is a descendant of one you first owned or were injured by. Perhaps it resembles your latest one. In any case your image lacks the sharpness of presence because the processes that inspect and operate upon the weakly-bound default features are very likely to change, adapt, or detach them.
Such default assignments would have subtle, idiosyncratic influences on the paths an individual would tend to follow in making analogies, generalizations, and judgements, especially when the exterior influences on such choices are weak. Properly chosen, such stereotypes could serve as a storehouse of valuable heuristic plan-skeletons; badly selected, they could form paralyzing collections of irrational biases. Because of them one might expect, as reported by Freud, to detect evidences of early cognitive structures in "free association" thinking.
1.12 FRAME-SYSTEMS AND PIAGET'S CONCRETE OPERATIONS
What, in effect, are the conditions for the construction of formal thought? The child must not only apply operations to objects–in other words, mentally execute possible actions on them–he must also 'reflect' those operations in the absence of the objects which are replaced by pure propositions. This 'reflection' is thought raised to the second power. Concrete thinking is the representation of a possible action, and formal thinking is the representation of a representation of possible action.
It is not surprising, therefore, that the system of concrete operations must be completed during the last years of childhood before it can be 'reflected' by formal operations. In terms of their function, formal operations do not differ from concrete operations except that they are applied to hypotheses or propositions whose logic is an abstract translation of the system of 'inference' that governs concrete operations." –J. Piaget, 1968 {The Mental Development of the Child}
I think there is a similarity between Piaget's idea of a concrete operation and the idea of applying a transformation between frames of a system. But other, more "abstract" kinds of reasoning should be much harder to do in such concrete ways. Similarly, some kinds of "logical" operations should be easy to perform with frames by substituting into loosely attached default assignments. It should be easy, for example, to approximate logical transitivity; thus surface syllogisms of the form
All A's are B's and All B's are C's
. ==>
All A's are C's
would occur in the natural course of substituting acceptable subframes into marked terminals of a frame. I do not mean that the generalization itself is asserted, but only that its content is applied to particular cases, because of the transitivity of instantiation of subframes. One would expect, then, also to find the same belief in
Most A's are B's and Most B's are C's
. ==>
Most A's are C's
even though this is sometimes false, as some adults have learned.
It would be valuable better to understand what can be done by simple processes working on frames. One could surely invent some "inference-frame technique" that could be used to rearrange terminals of other frames so as to simulate deductive logic. A major step in that direction, I think, is the "flat and cover" procedure proposed for Moore and Newell's MERLIN (1973). This is a procedure, related to logical "unification", whose output, given two frames A and B, is interpreted to mean (roughly): A can be viewed as a kind of B given a "mapping" or frame-transformation C that expresses (perhaps in terms of other mappings) how A's terminals can be viewed in terms of B's terminals. The same essay uses the view-changing concept to suggest a variety of new interpretations of such basic concepts as goal-direction, induction, and assimilation of new knowledge, and it makes substantial proposals about how the general frame idea might be realized in a computer program.
It appears that only with the emergence of Piaget's "formal" stage (for perspective, not usually until the second decade) are children reliably able to reason about, rather than with transformations. Nor do such capacities appear at once, or synchronously in all mental activities. To get greater reasoning power–and to be released from the useful but unreliable pseudo-logical of manipulating default assignments–one must learn the equivalent of operating on the transformations themselves. (One needs to get at the transformations because they contain knowledge needed for more sophisticated reasoning.) In a computational model constructed for Artificial Intelligence, one might try to make the system read its own programs. An alternative is to represent (redundantly) information about processes some other way. Workers on recent "program-understanding" programs in our laboratory have usually decided, for one reason or another, that programs should carry "commentaries" that express more directly their intentions, prerequisites, and effects; these commentaries are (at present) usually written in specialized sub-languages.
This raises an important point about the purpose of our theory. "schematic" thinking, based on matching complicated situations against stereotyped frame structures, must be inadequate for some aspects of mental activity. Obviously mature people can to some extent think about, as well as use their own representations. Let us speculatively interpret "formal operations" as processes that can examine and criticize our earlier representations (be they frame-like or whatever). With these we can begin to build up new structures to correspond to "representations of representations." I have no idea what role frame systems might play in these more complex activities.
The same strategy suggests that we identify (schematically, at least) the direct use of frames with Piaget's "concrete operations." If we do this then I find Piaget's explanation of the late occurrence of "formal thinking" paradoxically reassuring. In first trying to apply the frame-system paradigm to various problems, I was disturbed by how well it explained some things and how poorly others. But it was foolish to expect any single scheme to explain very much about thinking. Certainly one cannot expect to solve all the problems of sophisticated reasoning within a system confined to concrete operations–if that indeed amounts to the manipulation of stereotypes.
2 LANGUAGE, UNDERSTANDING, AND SCENARIOS
2.1 WORDS, SENTENCES AND MEANINGS
"The device of images has several defects that are the price of its peculiar excellences. Two of these are perhaps the most important: the image, and particularly the visual image, is apt to go farther in the direction of the individualization of situations than is biologically useful; and the principles of the combination of images have their own peculiarities and result in constructions which are relatively wild, jerky and irregular, compared with the straightforward unwinding of a habit, or with the somewhat orderly march of thought."– F. C. Bartlett {Remembering
The concepts of frame and default assignment seem helpful in discussing the phenomenology of "meaning." Chomsky (1957) points out that such a sentence as "colorless green ideas sleep furiously" is treated very differently than the non-sentence (B) "furiously sleep ideas green colorless"–and suggests that because both are "equally nonsensical," what is involved in the recognition of sentences must be quite different from what is involved in the appreciation of meanings.
There is no doubt that there are processes especially concerned with grammar. Since the meaning of an utterance is "encoded" as much in the positional and structural relations between the words as in the word choices themselves, there must be processes concerned with analyzing those relations in the course of building the structures that will more directly represent the meaning. What makes the words of (A) more effective and predictable than (B) in producing such a structure–putting aside the question of whether that structure should be called semantic or syntactic–is that the word-order relations in (A) exploit the (grammatical) convention and rules people usually use to induce others to make assignments to terminals of structures. This is entirely consistent with grammar theories. A generative grammar would be a summary description of the exterior appearance of those frame rules–or their associated processes–while the operators of transformational grammars seem similar enough to some of our frame transformations.
But one must also ask: to what degree does grammar have a separate identity in the actual working of a human mind? Perhaps the rejection of an utterance (either as non-grammatical, as nonsensical, or most important, as not understood , indicates a more complex failure of the semantic process to arrive at any usable representation; I will argue now that the grammar-meaning distinction may illuminate two extremes of a continuum, but obscures its all-important interior.
We certainly cannot assume that "logical" meaninglessness has a precise psychological counterpart. Sentence (A) can certainly generate an image! The dominant frame (in my case) is that of someone sleeping; the default system assigns a particular bed, and in it lies a mummy-like shape-frame with a translucent green color property. In this frame there is a terminal for the character of the sleep–restless, perhaps–and "furiously" seems somewhat inappropriate at that terminal, perhaps because the terminal does not like to accept anything so "intentional" for a sleeper. "Idea" is even more disturbing, because a person is expected, or at least something animate. I sense frustrated procedures trying to resolve these tensions and conflicts more properly, here or there, into the sleeping framework that has been evoked.
Utterance (B) does not get nearly so far because no subframe accepts any substantial fragment. As a result no larger frame finds anything to match its terminals, hence finally, no top level "meaning" or "sentence" frame can organize the utterance as either meaningful or grammatical. By combining this "soft" theory with gradations of assignment tolerances, I imagine one could develop systems that degrade properly for sentences with "poor" grammar rather than none; if the smaller fragments–phrases and sub-clauses–satisfy subframes well enough, an image adequate for certain kinds of comprehension could be constructed anyway, even though some parts of the top level structure are not entirely satisfied. Thus, we arrive at a qualitative theory of "grammatical": if the top levels are satisfied but some lower terminals are not we have a meaningless sentence; if the top is weak but the bottom solid, we can have an ungrammatical but meaningful utterance.
I do not mean to suggest that sentences must evoke visual images. Some people do not admit to assigning a color to the ball in "he kicked the ball." But everyone admits (eventually) to having assumed, if not a size or color, at least some purpose, attitude, or other elements of an assumed scenario. When we go beyond vision, terminals and their default assignments can represent purposes and functions, not just colors, sizes and shapes.
2.2 DISCOURSE
Linguistic activity involves larger structures than can be described in terms of sentential grammar, and these larger structures further blur the distinctness of the syntax-semantic dichotomy. Consider the following fable, as told by W. Chafe (Chafe 1972).
There was once a Wolf who saw a Lamb drinking at a river and wanted an excuse to eat it. For that purpose, even though he himself was upstream, he accused the Lamb of stirring up the water and keeping him from drinking...
To understand this, one must realize that the Wolf is lying! To understand the key conjunctive "even though" one must realize that contamination never flows upstream. This in turn requires us to understand (among other things) the word "upstream" itself. Within a declarative, predicate-based "logical" system, one might try to axiomatize "upstream" by some formula like:
. {A upstream B} AND {Event T, Stream muddy at A} ===>
Exists {Event U, Stream muddy at B} AND {Later U, T}
But an adequate definition would need a good deal more. What about the fact that the order of things being transported by water currents is not ordinarily changed? A logician might try to deduce this from a suitably intricate set of "local" axioms, together with appropriate "induction" axioms. I propose instead to represent this knowledge in a structure that automatically translocates spatial descriptions from the terminals of one frame to those of another frame of the same system. While this might be considered to be a form of logic, it uses some of the same mechanisms designed for spatial thinking.
In many instances we would handle a change over time, or a cause-effect relation, in the same way as we deal with a change in position. Thus, the concept river-flow could evoke a frame-system structure something like the following, where S1, S2, and S3 are abstract slices of the flowing river shown in figure 2.1.
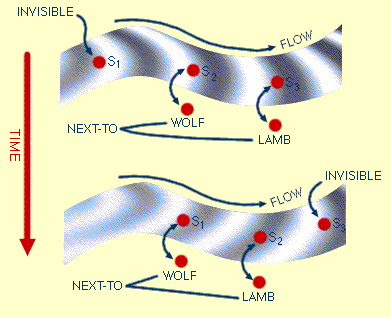
In my default system the Wolf is at the left, the Lamb at the right, and S1, S2, and S3 flow past them. In the diagram, presume that the S's cannot be seen unless they are directly next to either the wolf or the lamb. On reflection, my imaginary currents usually flow from left to right, and I find it some effort to use reversed versions. Perhaps they all descend from copies of the same proto-system.
The time (and not coincidentally, current) transformation represents part of our understanding of the effects of the flow of the river. If the terminal S3 is the mud effect produced by the Lamb, the frame system causes the mud-effect to become invisible and not-near the Wolf. Thus, he has no valid reason to complain. A more detailed system could have intermediate frames; in none of them is the Wolf contaminated.
There are many more nuances to fill in. What is "stirring up" and why would it keep the wolf from drinking? One might normally assign default floating objects to the S's, but here S3 interacts with "stirring up" to yield something that "drink" does not find acceptable. Was it "deduced" that stirring river-water means that S3 in the first frame should have "mud" assigned to it; or is this simply the default assignment for stirred water?
Almost any event, action, change, flow of material, or even flow of information can be represented to a first approximation by a two-frame generalized event. The frame-system can have slots for agents, tools, side-effects, preconditions, generalized trajectories, just as in the "trans" verbs of "case grammar" theories, but we have the additional flexibility of representing changes explicitly. To see if one has understood an event or action, one can try to build an appropriate instantiated frame-pair.
However, in representing changes by simple "before-after" frame-pairs, we can expect to pay a price. Pointing to a pair is not the same as describing their differences. This makes it less convenient to do planning or abstract reasoning; there is no explicit place to attach information about the transformation. As a second approximation, we could label pairs of nodes that point to corresponding terminals, obtaining structure like the "comparison-notes" in Winston (1970), or we might place at the top of the frame-system information describing the differences more abstractly. Something of this sort will be needed eventually.
In his work on "conceptual dependency," R. Schank (1972) attempts to represent meanings of complex assertions like
"Sam believes that John is a fool."
in which the thing that Sam believes is not an object but requires a "conceptualization" and even situations like that in
"Do you want a piece of chocolate?"
"No, I just had an ice cream cone."
in which understanding requires representing details of a complex notion of satiation. He proposes a small collection of "basic conceptualizations" and relations between them from which to build representations for any meaning. I find it hard to decide how adequate these are. How well, for example, could they describe flows?
Schank's schemes include an idea of "conceptual cases" which resemble some of our frame-terminals, but he attempts to represent the effects of actions as explicit abstractions rather than as relations between frame-like pairs. There are problems in this as well; one wonders how well a single abstract concept of cause (or even several) would suffice in a functioning "belief system." It certainly would not be enough to characterize causality only in terms of one condition or action being necessary for another to happen. Putting details aside, I think Schank has made a strong start and, once this area develops some performance tests, it should yield good knowledge-representation methods.
The work of Y. Wilks (1973) on "preference semantics" also seems rich in ideas about ways to build frame-like structures out of simpler ones, and his preference proposals embody specific ways one might represent default assignments and procedures for making them depend on larger aspects of a discourse than mere sentences. Wilks' system is interesting also in demonstrating, I think, ways in which one can get some useful informal reasoning, or pseudo-deduction as a product of the template building and instantiation processes without an elaborate formal logical system or undue concern with consistency.
R. P. Abelson (Abelson 1973) has worked toward representing even more extended activities. Beginning with elements like Schank's, he works out schemes in which the different concepts interact, arriving at intricate scripts ; skeletonized scenarios of elaborate belief systems, attempting even to portray such interactions as one's image of the role he plays in another person's plans.
D. McDermott (1973) discusses in his M.S. thesis many issues related to knowledge representations. In his scheme for plausible inference, statements are not simply accepted, but are subjected to a process of "doubting" and "believing"; in effect, things assumed by default (or plausibility) are retained with mechanisms for revising those beliefs when later, dependent assumptions run into problems. McDermott (1974) is particularly attentive to the problems involved in recovery from the errors any such system is forced to make in the course of informal, common sense inference. See also {Wilks, 1973}
2.3 MEANING-STRUCTURE OF A DISCOURSE
"Words... can indicate the qualitative and relational features of a situation in their general aspect just as directly as, and perhaps even more satisfactorily than, they can describe its particular individuality. This is, in fact, what gives to language its intimate relation to thought processes. For thinking, in the proper psychological sense, is never the mere reinstatement of some suitable past situation produced by a crossing of interests, but is the utilization of the past in solution of difficulties set by the present... Equally, nobody ever thinks who, being challenged, merely sets up an image from some more or less relevant situation, and then finds for himself a solution, without in any way formulating the relational principle involved." –F. C. Bartlett {Remembering}
"Case grammar" sentence-analysis theories such as those of Fillmore (1968) and Celce-Murcia (1972) involve structures somewhat like frames. Centered mainly around the verb, parts of a sentence are used to instantiate a sort of verb-frame in accord with various uses of prepositions. I agree that this surely is a real phenomenon; sentences are built around verbs, so it makes sense to use verb-centered frame-like structures for analyzing sentences.
In more extended discourse, however, I think that verb-centered structures often become subordinate or even disappear. The topic or "theme" of a paragraph is as likely to be a scene as to be an action, as likely to be a characterization of a person as to be something he is doing. Thus in understanding a discourse, the synthesis of a verb-structure with its case-assignments may be a necessary but transient phase. As sentences are understood, the resulting substructures must be transferred to a growing "scene-frame" to build up the larger picture. An action that is the chief concern of one sentence might, for example, become subsidiary to a characterization of one of the actors, in a larger story-frame.
I am not proposing anything like "verbs describe local (sentential) structures and nouns describe global (paragraphic) structures"–although that might be a conceptually useful first approximation. Any concept can be invoked by all sorts of linguistic representations. It is not a matter of nouns or verbs. The important point is that we must not assume that the transient semantic structure built during the syntactic analysis (what language theorists today call the "deep structure" of a sentence) is identical with the larger (and "deeper") structure built up incrementally as each fragment of a coherent linguistic communication operates upon it!
I do not want this emphasis on topical or thematic super-frames to suggest a radical confrontation between linguistic vs. non-linguistic representations. Introspectively, a substantial portion of common-sense thinking and reasoning seem to resemble linguistic transformations and other manipulations. The frames associated with word senses, be they noun, verb or whatever, are surely centers for the concentrated representation of vital knowledge about how different things are related, how they are used, and how they transform one another. Practically, there would be large advantages in having mechanisms that could use these same structures both for thinking and for communicating.
Let us imagine a frame-oriented scenario for how coherent discourse might be represented. At the start of a story, we know little other than that it will be a story, but even this gives us a start. A conventional frame for "story" (in general) would arrive with slots for setting, protagonists, main event, moral, etc. Indeed, the first line of a properly told story usually helps with the setting; the wolf and lamb story immediately introduces two antagonists, places them by the river (setting), and provides the wolf with a motive. The word "excuse" somehow prepares us for the likelihood of the wolf making false statements.
Each sentential analysis need be maintained only until its contents can be used to instantiate a larger structure. The terminals of the growing meaning-structure thus accumulate indicators and descriptors, which expect and key further assignments. A terminal that has acquired a "female person" marker will reject "male" pronominal assignments using, I suppose, the same sorts of considerations that resist assignment of tables and chairs to terminals of wall frames. As the story proceeds, information is transferred to super-frames whenever possible, instantiating or elaborating the scenario. In some cases we will be lucky enough to attach a whole subframe, for example, a description of the hero, to a single terminal in the super-frame. This could happen if a terminal of the "story" super-frame matches a top level indicator on the current sentence-frame. Other sentences might produce relations constraining pairs of already existing terminals. But what if no such transfer can be made because the listener expected a wrong kind of story and has no terminals to receive the new structure?
We go on to suppose that the listener actually has many story frames, linked by the kinds of retrieval structures discussed later on. First we try to fit the new information into the current story-frame. If we fail, we construct an error comment like "there is no place here for an animal." This causes us to replace the current story-frame by, say, an animal-story frame. The previous assignments to terminals may all survive, if the new story frame has the same kinds of terminals. But if many previous assignments do not so transfer, we must get another new story-frame. If we fail, we must either construct a basically new story-frame–a major intellectual event, perhaps–or just give up and forget the assignments. (Presumably that is the usual reaction to radically new narrative forms! One does not learn well if the required jumps are too large: one cannot really understand animal stories until one possesses the conventional personality frames for the wolf, pig, fox, etc.)
Thus a discourse assembles a network of instantiated frames and subframes. Attributive or descriptive information can often be represented by simple sub-structures, but actions, temporal successions, explanations and other complicated things surely need more elaborate attachments. We must recognize that profoundly hard questions, central to epistemology as well as to linguistics, are entrained in this problem of how to merge information from different sources and subframes. The next few sections raise more questions about these than they begin to answer.
2.4 LANGUAGE TRANSLATION
Translation affords an opportunity to observe defaults at work. In translating the story about the wolf and the lamb from English to Japanese, according to Chafe, it is required to mention the place on the river where the actors stand, although it is not required in English. In English one must cite the time–if only by saying "Once...." In Japanese, it is customary to characterize the place, as well as the time, even if only by a nonspecific "In a certain place...."
I think that both place and time are required, in the deeper meaning-frames of people who think much as we do whatever natural language they speak! Hence, default assignments for both would be immediately available to the translator if he understood the sentence at all. Good simultaneous translators proceed so rapidly that one wonders how much they can really understand before speaking; our theory makes this less of an issue because, if the proper frame is retrieved in the course of partial understanding, its default assignments are available instantly, before the more complex assignment negotiations are completed.
A translation of "The Wolf and Lamb" into Japanese with acceptable surface structure might be, according to Chafe,
Once certain place in river at water drinking be child-sheep saw one animal wolf was and that wolf that child-sheep eat for excuse make-want-seeming was....
It is more natural, in Japanese, to say what the Lamb was drinking than just to say he was drinking. Here is one way that language affects thinking: each such linguistic convention focuses special attention on filling certain terminals. If water is the usual thing to drink in one's culture, then water is the default assignment for what is being drunk. When speech production requires such an assignment in a sentence-output frame, that default will normally be assumed. Of course, one should be even more certain of water if the drinking is done beside a river; this needs some machinery for relating drinking and river stereotypes. It seems clear that if there is a weakly-bound drinkable-fluid slot in one frame, and a strongly-bound drinkable fluid in the subframe to be attached, the latter should dislodge the former. Thus, even if our listener usually drinks wine, he should correctly imagine the lamb drinking water.
2.5 ACTIVE VS. PASSIVE
In our traditional "folk phenomenology," Seeing and Imagining are usually seen as "passive" and "active." It is tempting to exploit this viewpoint for vision:
In seeing, one analyses a scene by assembling and instantiating frames, generally without much choice because of the domination of the need to resolve "objective" visual evidence against the need for a consistent and plausible spatial scene-description.
In imagining, we have much more choice, for we are trying to assemble and instantiate frames to represent a "scene" that satisfies internally chosen–hence changeable–goals.
In language, a similar contrast is tempting:
In listening, which includes parsing, one has little choice because of the need to resolve the objective word string into a structure consistent with grammar, context, and the assumed intention.
In speaking, we have much more choice, because there are so many ways to assemble sentence-making frames for our chosen purpose, be it to inform, convince, or mislead.
However, these are dangerous oversimplifications; things are often quite the other way around! Speaking is often a straightforward encoding from a semantic structure into a word sequence, while listening often involves extensive and difficult constructions –which involve the totality of complexities we call understanding.
Consider the analogy between a frame for a room in a visual scene and a frame for a noun-phrase in a discourse.
In each case, some assignments to terminals are mandatory, while others are optional. A wall need not be decorated, but every moveable object must be supported. A noun phrase need not contain a numerical determiner, but it must contain a noun or pronoun equivalent. One generally has little choice so far as surface structure is concerned: one must account for all the words in a sentence and for all the major features of a scene.
But surface structure is not everything in vision or in language. One has unlimited options about incorporating consequences of context and knowledge into semantic structure. An object has not only a visual form, but a history. Its presence has usually a cause and often some other significance–perhaps as a clue in a puzzle, or as a symbol of a changing relationship.
Any sentence can be understood in many ways. I emphasize that I am not talking of the accidental (and relatively unimportant) ambiguities of parsing, but of the purposeful variations of interpretation. Just as any room can be seen from different physical viewpoints, so any assertion can be "viewed" from different representational viewpoints as in the following, each of which suggests a different structure:
He kicked the ball.
The ball was kicked.
There was some kicking today.
Because such variations formally resemble the results of the syntactic, active-passive operations of transformational grammars, one might overlook their semantic significance. We select one or the other in accord with thematic issues– on whether one is concerned with what "he" did, with finding a lost ball, with who damaged it, or whatever. One answers such questions most easily by bringing the appropriate entity or action into the focus of attention, by evoking a frame primarily concerned with that topic.
In the traditional view of transformational linguistics, these alternate frames have no separate existence but are only potential derivatives from a single deep structure. There is an advantage to supposing their separate existence in long term memory: we could attach specific knowledge to each about how it should be used. However, as language theorists rightly point out, there are systematic regularities which suggest that such "transformations" are nearly as readily applied to unfamiliar verbs with the same redirections of concern; this makes separate existence less plausible. I have the impression that transformational theorists tend to believe in some special central mechanisms for management of such changes of "semantic perspective," even though, I should think, the variety of idiosyncrasies attached to individual words makes this technically difficult. A theory more in the spirit of this essay would suggest that whenever one encounters an unfamiliar usage (or an unfamiliar word) he applies some matching process to guess–rightly or wrongly–which familiar usage it resembles, and then adapts the existing attention-transformation system for that word. I cannot see what kind of experiment might distinguish between these conjectures, but I still feel that the distinction is important.
Some readers might object that things should not be so complicated–that we need a simpler theory–if only to explain how people understand sentences so quickly. One must not forget that it often takes minutes, hours, or forever, to understand something.
2.6 SCENARIOS
"Thinking... is biologically subsequent to the image-forming process. It is possible only when a way has been found of breaking up the 'massed' influence of past stimuli and situations, only when a device has already been discovered for conquering the sequential tyranny of past reactions. But though it is a later and a higher development, it does not supercede the method of images. It has its own drawbacks. Contrasted with imaging it loses something of vivacity, of vividness, of variety. Its prevailing instruments are words, and, not only because these are social, but also because in use they are necessarily strung out in sequence, they drop into habit reactions even more readily than images do. With thinking we run greater and greater risk of being caught up in generalities that may have little to do with actual concrete experience. If we fail to maintain the methods of thinking, we run the risks of becoming tied to individual instances and of being made sport of by the accidental circumstances belonging to these." –F. C. Bartlett {Remembering}
We condense and conventionalize, in language and thought, complex situations and sequences into compact words and symbols. Some words can perhaps be "defined" in elegant, simple structures, but only a small part of the meaning of "trade" is captured by
. first frame –––––> second frame
. A has X B has Y B has X A has Y}
Trading normally occurs in a social context of law, trust and convention. Unless we also represent these other facts, most trade transactions will be almost meaningless. It is usually essential to know that each party usually wants both things but has to compromise. It is a happy but unusual circumstance in which each trader is glad to get rid of what he has. To represent trading strategies, one could insert the basic maneuvers right into the above frame-pair scenario: in order for A to make B want X more (or want Y less) we expect him to select one of the familiar tactics:
Offer more for Y.
Explain why X is so good.
Disparage the competition.
Make B think C wants X.
These only scratch the surface. Trades usually occur within a scenario tied together by more than a simple chain of events each linked to the next. No single such scenario will do; when a clue about trading appears it is essential to guess which of the different available scenarios is most likely to be useful.
Charniak's thesis (1972) studies questions about transactions that seem easy for people to comprehend yet obviously need rich default structures. We find in elementary school reading books such stories as:
She wondered if he would like a kite.
She went to her room and shook her piggy bank.
It made no sound.
Most young readers understand that Jane wants money to buy Jack a kite for a present but that there is no money to pay for it in her piggy bank. Charniak proposes a variety of ways to facilitate such inferences–a "demon" for present that looks for things concerned with money, a demon for "piggy bank" which knows that shaking without sound means the bank is empty, etc. But although present now activates money, the reader may be surprised to find that neither of those words (nor any of their synonyms) occurs in the story. "Present" is certainly associated with "party" and "money" with "bank," but how are the longer chains built up? Here is another problem raised in Charniak. A friend tells Jane:
He already has a Kite.
He will make you take it back.
Take which kite back? We do not want Jane to return Jack's old kite. To determine the referent of the pronoun "it" requires understanding a lot about an assumed scenario. Clearly, "it" refers to the proposed new kite. How does one know this? (Note that we need not agree on any single explanation.) Generally, pronouns refer to recently mentioned things, but as this example shows, the referent depends on more than the local syntax.
Suppose for the moment we are already trying to instantiate a "buying a present" default subframe. Now, the word "it" alone is too small a fragment to deal with, but "take it back" could be a plausible unit to match a terminal of an appropriately elaborate buying scenario. Since that terminal would be constrained to agree with the assignment of "present" itself, we are assured of the correct meaning of it in "take X back." Automatically, the correct kite is selected. Of course, that terminal will have its own constraints as well; a subframe for the "take it back" idiom should know that "take X back" requires that:
X was recently purchased.
The return is to the place of purchase.
You must have your sales slip. Etc.
If the current scenario does not contain a "take it back" terminal, then we have to find one that does and substitute it, maintaining as many prior assignments as possible. Notice that if things go well the question of it being the old kite never even arises. The sense of ambiguity arises only when a "near miss" mismatch is tried and rejected.
Charniak's proposed solution to this problem is in the same spirit but emphasizes understanding that because Jack already has a kite, he may not want another one. He proposes a mechanism associated with "present":
(A) If we see that a person P might not like a present X, then look for X being returned to the store where it was bought.
(B) If we see this happening, or even being suggested, assert that the reason why is that P does not like X.
This statement of "advice" is intended by Charniak to be realized as a production-like entity to be added to the currently active data-base whenever a certain kind of context is encountered. Later, if its antecedent condition is satisfied, its action adds enough information about Jack and about the new kite to lead to a correct decision about the pronoun.
Charniak in effect proposes that the system should watch for certain kinds of events or situations and inject proposed reasons, motives, and explanations for them. The additional interconnections between the story elements are expected to help bridge the gaps that logic might find it hard to cross, because the additions are only "plausible" default explanations, assumed without corroborative assertions. By assuming (tentatively) "does not like X" when X is taken back, Charniak hopes to simulate much of ordinary "comprehension" of what is happening. We do not yet know how complex and various such plausible inferences must be to get a given level of performance, and the thesis does not answer this because it did not include a large simulation. Usually he proposes terminating the process by asserting the allegedly plausible motive without further analysis unless necessary. To understand why Jack might return the additional kite it should usually be enough to assert that he does not like it. A deeper analysis might reveal that Jack would not really mind having two kites but he probably realizes that he will get only one present; his utility for two different presents is probably higher.
2.7 SCENARIOS AND "QUESTIONS"
The meaning of a child's birthday party is very poorly approximated by any dictionary definition like "a party assembled to celebrate a birthday," where a party would be defined, in turn, as "people assembled for a celebration." This lacks all the flavor of the culturally required activities. Children know that the "definition" should include more specifications, the particulars of which can normally be assumed by way of default assignments:
DRESS ––––– SUNDAY BEST.
PRESENT ––– MUST PLEASE HOST. MUST BE BOUGHT AND GIFT-WRAPPED.
GAMES ––––– HIDE AND SEEK. PIN TAIL ON DONKEY.
DECOR ––––– BALLOONS. FAVORS. CREPE-PAPER.
PARTY-MEAL–CAKE. ICE-CREAM. SODA. HOT DOGS.
CAKE ––––– CANDLES. BLOW-OUT. WISH.
SING BIRTHDAY SONG.
ICE-CREAM –– STANDARD THREE-FLAVOR.
These ingredients for a typical American birthday party must be set into a larger structure. Extended events take place in one or more days. A Party takes place in a Day, of course, and occupies a substantial part of it, so we locate it in an appropriate day frame. A typical day has main events such as
Get-up Dress Eat-1 Go-to-Work Eat-2...
but a School-Day has more fixed detail:
Get-up Dress
. Eat-1 Go-to-School Be-in-School
. Home-Room Assembly English Math (arrgh)
. Eat-2 Science Recess Sport
. Go-Home Play
. Eat-3 Homework Go-To-Bed
Birthday parties obviously do not fit well into school-day frames. Any parent knows that the Party-Meal is bound to Eat-2 of its Day. I remember a child who did not seem to realize this. Absolutely stuffed after the Party-Meal, he asked when he would get Lunch.
Returning to Jane's problem with the kite, we first hear that she is invited to Jack's Birthday Party. Without the party scenario, or at least an invitation scenario, the second line seems rather mysterious:
She wondered if he would like a kite.
To explain one's rapid comprehension of this, I will make a somewhat radical proposal: to represent explicitly, in the frame for a scenario structure, pointers to a collection of the most serious problems and questions commonly associated with it.
In fact we shall consider the idea that the frame terminals are exactly those questions.
Thus, for the birthday party:
Y must get P for X ––––– Choose P!
. X must like P ––––––––– Will X like P?
. Buy P ––––––––––– Where to buy P?
. Get money to buy P ––– Where to get money?
. (Sub-questions of the "present" frame?)
. Y must dress up ––––––– What should Y wear?
Certainly these are one's first concerns, when one is invited to a party.
The reader is free to wonder, with the author, whether this solution is acceptable. The question, "Will X like P?" certainly matches "She wondered if he would like a kite?" and correctly assigns the kite to P. But is our world regular enough that such question sets could be pre-compiled to make this mechanism often work smoothly? I think the answer is mixed. We do indeed expect many such questions; we surely do not expect all of them. But surely "expertise" consists partly in not having to realize, ab initio what are the outstanding problems and interactions in situations. Notice, for example, that there is no default assignment for the Present in our party-scenario frame. This mandates attention to that assignment problem and prepares us for a possible thematic concern. In any case, we probably need a more active mechanism for understanding "wondered" which can apply the information currently in the frame to produce an expectation of what Jane will think about.
The third line of our story, about shaking the bank, should also eventually match one of the present-frame questions, but the unstated connection between Money and Piggy-Bank is presumably represented in the piggy-bank frame, not the party frame, although once it is found it will match our Get-Money question terminal. The primary functions and actions associated with piggy banks are Saving and Getting-Money-Out, and the latter has three principal methods:
1. Using a key. Most piggy banks don't offer this option.
2. Breaking it. Children hate this.
3. Shaking the money out, or using a thin slider.
In the fourth line does one know specifically that a silent Bank is empty, and hence out of money (I think, yes) or does one use general knowledge that a hard container which makes no noise when shaken is empty? I have found quite a number of people to prefer the latter. Logically the "general principle" would indeed suffice, but I feel that this misses the important point that a specific scenario of this character is engraved in every child's memory. The story is instantly intelligible to most readers. If more complex reasoning from general principles were required this would not be so, and more readers would surely go astray. It is easy to find more complex problems:
A goat wandered into the yard where Jack was painting. The goat got the paint all over himself. When Mother saw the goat she asked, "Jack, did you do that?
There is no one word or line, which is the referent of "that." It seems to refer, as Charniak notes, to "cause the goat to be covered with paint." Charniak does not permit himself to make a specific proposal to handle this kind of problem, remarking only that his "demon" model would need a substantial extension to deal with such a poorly localized "thematic subject." Consider how much one has to know about our culture, to realize that that is not the goat-in-the-yard but the goat-covered-with-paint. Charniak's thesis–basically a study rather than a debugged system–discusses issues about the activation, operation, and dismissal of expectation and default-knowledge demons. Many of his ideas have been absorbed into this essay.
In spite of its tentative character, I will try to summarize this image of language understanding as somewhat parallel to seeing. The key words and ideas of a discourse evoke substantial thematic or scenario structures, drawn from memory with rich default assumptions. The individual statements of a discourse lead to temporary representations–which seem to correspond to what contemporary linguists call "deep structures"–which are then quickly rearranged or consumed in elaborating the growing scenario representation. In order of "scale," among the ingredients of such a structure there might be these kinds of levels:
Surface Syntactic Frames
–– Mainly verb and noun structures. Prepositional and word-order indicator conventions.
Surface Semantic Frames
––Action-centered meanings of words. Qualifiers and relations concerning participants, instruments, trajectories and strategies, goals, consequences and side-effects.
Thematic Frames
–– Scenarios concerned with topics, activities, portraits, setting. Outstanding problems and strategies commonly connected with topic.
Narrative Frames
–– Skeleton forms for typical stories, explanations, and arguments. Conventions about foci, protagonists, plot forms, development, etc., designed to help a listener construct a new, instantiated Thematic Frame in his own mind.
A single sentence can assign terminals, attach subframes, apply a transformation, or cause a gross replacement of a high level frame when a proposed assignment no longer fits well enough. A pronoun is comprehensible only when general linguistic conventions, interacting with defaults and specific indicators, determine a terminal or subframe of the current scenario.
In vision the transformations usually have a simple group-like structure. In language we expect more complex, less regular systems of frames. Nevertheless, because time, cause, and action are so important to us, we often use sequential transformation pairs that replace situations by their temporal or causal successors.
Because syntactic structural rules direct the selection and assembly of the transient sentence frames, research on linguistic structures should help us understand how our frame systems are constructed. One might look for such structures specifically associated with assigning terminals, selecting emphasis or attention viewpoints (transformations), inserting sentential structures into thematic structures, and changing gross thematic representations.
Finally, just as there are familiar "basic plots" for stories, there must be basic super-frames for discourses, arguments, narratives, and so forth. As with sentences, we should expect to find special linguistic indicators for operations concerning these larger structures; we should move beyond the grammar of sentences to try to find and systematize the linguistic conventions that, operating across wider spans, must be involved with assembling and transforming scenarios and plans.
2.8 QUESTIONS, SYSTEMS, AND CASES
"Questions arise from a point of view–from something that helps to structure what is problematical, what is worth asking, and what constitutes an answer (or progress). It is not that the view determines reality, only what we accept from reality and how we structure it. I am realist enough to believe that in the long run reality gets its own chance to accept or reject our various views. –A. Newell {Artificial Intelligence and the Concept of Mind}
Examination of linguistic discourse leads thus to a view of the frame concept in which the "terminals" serve to represent the questions most likely to arise in a situation. To make this important viewpoint more explicit, we will spell out this reinterpretation.
A Frame is a collection of questions to be asked about a hypothetical situation; it specifies issues to be raised and methods to be used in dealing with them.
The terminals of a frame correspond perhaps to what Schank (Schank 1973) calls "conceptual cases", although I do not think we should restrict them to so few types as Schank suggests. To understand a narrated or perceived action, one often feels compelled
to ask such questions as
What caused it (agent)?
What was the purpose (intention)?
What are the consequences (side-effects)?
Who does it affect (recipient)?
How is it done (instrument)?
The number of such "cases" or questions is problematical. While we would like to reduce meaning to a very few "primitive" concepts, perhaps in analogy to the situation in traditional linguistic analysis, I know of no reason to suppose that that goal can be achieved. My own inclination is to side with such workers as W. Martin (1974), who look toward very large collections of "primitives," annotated with comments about how they are related. Only time will tell which is better.
For entities other than actions one asks different questions; for thematic topics the questions may be much less localized, e.g.,
Why are they telling this to me? How can I find out more about t? How will it help with the "real problem"?
and so forth. In a "story" one asks what is the topic, what is the author's attitude, what is the main event, who are the protagonists and so on. As each question is given a tentative answer the corresponding subframes are attached and the questions they ask become active in turn.
The "markers" we proposed for vision-frames become more complex in this view. If we adopt for the moment Newell's larger sense of "view", it is not enough simply to ask a question; one must indicate how it is to be answered. Thus a terminal should also contain (or point to) suggestions and recommendations about how to find an assignment. Our "default" assignments then become the simplest special cases of such recommendations, and one certainly could have a hierarchy in which such proposals depend on features of the situation, perhaps along the lines of Wilks' (Wilks 1973) "preference" structures.
For syntactic frames, the drive toward ritualistic completion of assignments is strong, but we are more flexible at the conceptual level. As Schank (1973) says,
"People do not usually state all the parts of a given thought that they are trying to communicate because the speaker tries to be brief and leaves out assumed or unessential information {...}. The conceptual processor makes use of the unfilled slots to search for a given type of information in a sentence or a larger unit of discourse that will fill the needed slot".
Even in physical perception we have the same situation. A box will not present all of its sides at once to an observer, and while this is certainly not because it wants to be brief, the effect is the same; the processor is prepared to find out what the missing sides look like and (if the matter is urgent enough) to move around to find answers to such questions.
Frame-Systems, in this view, become choice-points corresponding (on the conceptual level) to the mutually exclusive choice "Systems" exploited by Winograd (1970). The different frames of a system represent different ways of using the same information, located at the common terminals. As in the grammatical situation, one has to choose one of them at a time. On the conceptual level this choice becomes: what questions shall I ask about this situation?
View-changing, as we shall argue, is a problem-solving technique important in representing, explaining, and predicting. In the rearrangements inherent in the frame-system representation (for example, of an action) we have a first approximation to Simmons' (1973) idea of "procedures which in some cases will change the contextual definitional structure to reflect the action of a verb". Where do the "questions" come from? This is not in the scope of this paper, really, but we can be sure that the frame-makers (however they operate) must use some principles. The methods used to generate the questions ultimately shape each person's general intellectual style. People surely differ in details of preferences for asking "Why?", "How can I find out more?", "What's in it for me?", "How will this help with the current higher goals?", and so forth.
Similar issues about the style of answering must arise. In its simplest form the drive toward instantiating empty terminals would appear as a variety of hunger or discomfort, satisfied by any default or other assignment that does not conflict with a prohibition. In more complex cases we should perceive less animalistic strategies for acquiring deeper understandings.
It is tempting, then, to imagine varieties of frame-systems that span from simple template-filling structures to implementations of the "views" of Newell–with all their implications about coherent generators of issues with which to be concerned, ways to investigate them, and procedures for evaluating proposed solutions. But as I noted in 1.12, I feel uncomfortable about any superficially coherent synthesis in which one expects the same kind of theoretical framework to function well on many different levels of scale or concept. We should expect very different question-processing mechanisms to operate our low-level stereotypes and our most comprehensive strategic overviews.
3 LEARNING, MEMORY, AND PARADIGMS
"To the child, Nature gives various means of rectifying any mistakes he may commit respecting the salutary or hurtful qualities of the objects which surround him. On every occasion his judgements are corrected by experience; want and pain are the necessary consequences arising from false judgement; gratification and pleasure are produced by judging aright. Under such masters, we cannot fail but to become well informed; and we soon learn to reason justly, when want and pain are the necessary consequences of a contrary conduct.
In the study and practice of the sciences it is quite different; the false judgements we form neither affect our existence nor our welfare; and we are not forced by any physical necessity to correct them. Imagination, on the contrary, which is ever wandering beyond the bounds of truth, joined to self-love and that self-confidence we are so apt to indulge, prompt us to draw conclusions that are not immediately derived from facts...."}–A. Lavoisier {Elements of Chemistry}
How does one locate a frame to represent a new situation? Obviously, we cannot begin any complete theory outside the context of some proposed global scheme for the organization of knowledge in general. But if we imagine working within some bounded domain we can discuss some important issues:
EXPECTATION: How to select an initial frame to meet some given conditions.
ELABORATION: How to select and assign subframes to represent additional details.
ALTERATION: How to find a frame to replace one that does not fit well enough.
NOVELTY: What to do if no acceptable frame can be found. Can we modify an old frame or must we build a new one?
LEARNING: What frames should be stored, or modified, as a result of the experience?
In popular culture, memory is seen as separate from the rest of thinking; but finding the right memory–it would be better to say: finding a useful memory–needs the same sorts of strategies used in other kinds of thinking!
We say someone is "clever" who is unusually good at quickly locating highly appropriate frames. His information retrieval systems are better at making good hypotheses, formulating the conditions the new frame should meet, and exploiting knowledge gained in the "unsuccessful" part of the search. Finding the right memory is no less a problem than solving any other kind of puzzle! Because of this, a good retrieval mechanism can be based only in part upon basic "innate" mechanisms. It must also depend largely on (learned) knowledge about the structure of one's own knowledge! Our proposal will combine several elements–a Pattern Matching Process, a Clustering Theory, and a Similarity Network.
In seeing a room, or understanding a story, one assembles a network of frames and subframes. Everything noticed or guessed, rightly or wrongly, is represented in this network. We have already suggested that an active frame cannot be maintained unless its terminal conditions are satisfied.
We now add the postulate that all satisfied frames must be assigned to terminals of superior frames. This applies, as a special case, to any substantial fragments of "data" that have been observed and represented.
Of course, there must be an exception! We must allow a certain number of items to be attached to something like a set of "short term memory" registers. But the intention is that very little can be remembered unless embedded in a suitable frame. This, at any rate, is the conceptual scheme; in particular domains we would of course admit other kinds of memory "hooks" and special sensory buffers.
3.1 REQUESTS TO MEMORY
We can now imagine the memory system as driven by two complementary needs. On one side are items demanding to be properly represented by being embedded into larger frames; on the other side are incompletely-filled frames demanding terminal assignments. The rest of the system will try to placate these lobbyists, but not so much in accord with "general principles" as in accord with special knowledge and conditions imposed by the currently active goals.
When a frame encounters trouble–when an important condition cannot be satisfied–something must be done. We envision the following major kinds of accommodation to trouble.
MATCHING: When nothing more specific is found, we can attempt to use some "basic" associative memory mechanism. This will succeed by itself only in relatively simple situations, but should play a supporting role in the other tactics.
EXCUSE: An apparent misfit can often be excused or explained. A "chair" that meets all other conditions but is much too small could be a "toy."
ADVICE: The frame contains explicit knowledge about what to do about the trouble. Below, we describe an extensive, learned, "Similarity Network" in which to embed such knowledge.
SUMMARY: If a frame cannot be completed or replaced, one must give it up. But first one must construct a well-formulated complaint or summary to help whatever process next becomes responsible for reassigning the subframes left in limbo.
In my view, all four of these are vitally important. I discuss them in the following sections.
3.2 MATCHING
When replacing a frame, we do not want to start all over again. How can we remember what was already "seen?" We consider here only the case in which the system has no specific knowledge about what to do and must resort to some "general" strategy. No completely general method can be very good, but if we could find a new frame that shares enough terminals with the old frame, then some of the common assignments can be retained, and we will probably do better than chance.
The problem can be formulated as follows: let E be the cost of losing a certain already assigned terminal and let F be the cost of being unable to assign some other terminal. If E is worse than F, then any new frame should retain the old subframe. Thus, given any sort of priority ordering on the terminals, a typical request for a new frame should include:
1) Find a frame with as many terminals in common with {a,b,...,z} as possible, where we list high priority terminals already assigned in the old frame.
But the frame being replaced is usually already a subframe of some other frame and must satisfy the markers of its attachment terminal, lest the entire structure be lost. This suggests another form of memory request, looking upward rather than downward:
(2) Find or build a frame that has properties {a,b,...,z}
If we emphasize differences rather than absolute specifications, we can merge (2) and (1):
(3) Find a frame that is like the old frame except for certain differences {a,b,...,z} between them.
One can imagine a parallel-search or hash-coded memory to handle (1) and (2) if the terminals or properties are simple atomic symbols. (There must be some such mechanism, in any case, to support a production-based program or some sort of pattern matcher.) Unfortunately, there are so many ways to do this that it implies no specific design requirements.
Although (1) and (2) are formally special cases of (3), they are different in practice because complicated cases of (3) require knowledge about differences. In fact (3) is too general to be useful as stated, and I will later propose to depend on specific, learned, knowledge about differences between pairs of frames rather than on broad, general principles.
It should be emphasized again that we must not expect magic. For difficult, novel problems a new representation structure will have to be constructed, and this will require application of both general and special knowledge. The paper of Freeman and Newell (1971) discusses the problem of design of structures. That paper complements this one in an important dimension, for it discusses how to make a structure that satisfies a collection of functional requirements–conditions related to satisfying goals–in addition to conditions on containment of specified substructures and symbols. {Freeman and Newell, 1971}
3.3 EXCUSES
We can think of a frame as describing an "ideal." If an ideal does not match reality because it is "basically" wrong, it must be replaced. But it is in the nature of ideals that they are really elegant simplifications; their attractiveness derives from their simplicity, but their real power depends upon additional knowledge about interactions between them! Accordingly we need not abandon an ideal because of a failure to instantiate it, provided one can explain the discrepancy in terms of such an interaction. Here are some examples in which such an "excuse" can save a failing match:
OCCLUSION: A table, in a certain view, should have four legs, but a chair might occlude one of them. One can look for things like T-joints and shadows to support such an excuse.
FUNCTIONAL VARIANT: A chair-leg is usually a stick, geometrically; but more important, it is functionally a support. Therefore, a strong center post, with an adequate base plate, should be an acceptable replacement for all the legs. Many objects are multiple purpose and need functional rather than physical descriptions.
BROKEN: A visually missing component could be explained as in fact physically missing, or it could be broken. Reality has a variety of ways to frustrate ideals.
PARASITIC CONTEXTS: An object that is just like a chair, except in size, could be (and probably is) a toy chair. The complaint "too small" could often be so interpreted in contexts with other things too small, children playing, peculiarly large "grain," and so forth.
In most of those examples, the kinds of knowledge to make the repair–and thus salvage the current frame–are "general" enough usually to be attached to the thematic context of a superior frame. In the remainder of this essay, I will concentrate on types of more sharply localized knowledge that would naturally be attached to a frame itself, for recommending its own replacement.
3.4 SIMILARITY NETWORKS
"The justification of Napoleon's statement–if, indeed, he ever made it–that those who form a picture of everything are unfit to command, is to be found in the first of these defects. A commander who approaches a battle with a picture before him of how such and such a fight went on such and such an occasion, will find, two minutes after the forces have joined, that something has gone awry. Then his picture is destroyed. He has nothing in reserve except another individual picture and this also will not serve him for long. Or it may be that when his first pictured forecast is found to be inapplicable, he has so multifarious and pressing a collection of pictures that equally he is at a loss what practical adjustment to make. Too great individuality of past reference may be very nearly as embarrassing as no individuality of past reference at all. To serve adequately the demands of a constantly changing environment, we have not only to pick items out of their general setting, but we must know what parts of them may flow and alter without disturbing their general significance and functions."–F. C. Bartlett {Remembering}
In moving about a familiar house, we already know a dependable structure for "information retrieval" of room frames. When we move through Door D, in Room X, we expect to enter Room Y (assuming D is not the Exit). We could represent this as an action transformation of the simplest kind, consisting of pointers between pairs of room frames of a particular house system.
When the house is not familiar, a "logical" strategy might be to move up a level of classification: when you leave one room, you may not know which room you are entering, but you usually know that it is some room. Thus, one can partially evade lack of specific information by dealing with classes–and one has to use some form of abstraction or generalization to escape the dilemma of Bartlett's commander.
In some sense the use of classes is inescapable; when specific information is unavailable, one turns to classes as a "first-order" theory underlying any more sophisticated model. Fortunately, it is not necessary to use classes explicitly; indeed, that leads to trouble! While "class," taken literally or mathematically, forces one into an inclusion-based hierarchy, "concepts" are interrelated in different ways when in different contexts, and no single hierarchical ordering is generally satisfactory for all goals. This observation holds also for procedures and for frames. We do not want to be committed to an inflexible, inclusion-oriented classification of knowledge.
Winston's thesis (1970) proposes a way to construct a retrieval system that can represent classes but has additional flexibility. His retrieval pointers can be made to represent goal requirements and action effects as well as class memberships. Because the idea is not well-known, I will explain it by elaborating an example sketched in his thesis:
What does it mean to expect a chair? Typically, four legs, some assortment of rungs, a level seat, an upper back. One expects also certain relations between these "parts." The legs must be below the seat, the back above. The legs must be supported by the floor. The seat must be horizontal, the back vertical, and so forth.
Now suppose that this description does not match; the vision system finds four legs, a level plane, but no back. The "difference" between what we expect and what we see is "too few backs." This suggests not a chair, but a table or a bench.
Winston proposes pointers from each description in memory to other descriptions, with each pointer labeled by a difference marker. Complaints about mismatch are matched to the difference pointers leaving the frame and thus may propose a better candidate frame. Winston calls the resulting structure a "Similarity Network".
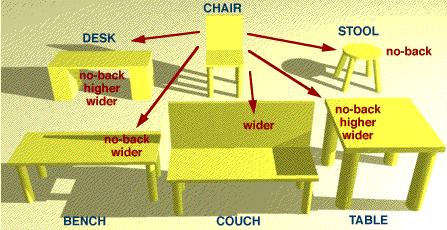
A furniture network with Chair, Couch. Table, Stool, Desk, etc., and their similarities and differences. A table is to high to serve as a chair, a box has no room for the knees, etc.
Winston proposes, incidentally, that a machine might spend idle time in an orderly comparison of various models in memory with one another. Whenever it finds few important differences between a pair, it inserts difference pointers for them.
But difference information becomes available also in any attempt to match a situation with memory, as successive attempts yield models that are generally similar but have specific, describable differences. Thus, instead of wasting this information one can use it to make the Similarity Network structure grow in the course of normal use of memory. If this pointer-building procedure is sensible about recording differences "relevant" to achieving goals, the result will be so much the more useful, and we have a mechanism for learning from experience.
Is a Similarity Network practical? At first sight, there might seem to be a danger of unconstrained growth of memory. If there are N frames, and K kinds of differences, then there could be as many as KN2 inter-frame pointers. One might fear the following consequences:
(1) If N is large, say 107, then N2is very large–of the order of 1014– which might be impractical, at least for human memory.
(2) There might be so many pointers for a given difference and a given frame that the system will not be selective enough to be useful.
(3) K itself might be very large if the system is sensitive to many different kinds of issues.
Actually, none of these problems seem really serious in connection with human memory. According to contemporary opinions (admittedly, not very conclusive) about the rate of storage into human long-term memory there are probably not enough seconds in a lifetime to cause a saturation problem.
In regard to (2), most pairs of frames that make up the N2 term should be so different that no plausible comparison mechanism should consider inserting any pointers at all between them. As Winston notes, only a "near miss" is likely to be of much value. Certainly, excessive reliance on undiscriminating differences will lead to confusion.
So the real problem, paradoxically, is that there will be too few connections! One cannot expect to have enough time to fill out the network to saturation. Given two frames that should be linked by a difference, we cannot count on that pointer being there; the problem may not have occurred before. However, in the next section we see how to partially escape this problem.
3.5 CLUSTERS, CLASSES, AND A GEOGRAPHIC ANALOGY
"Though a discussion of some of the attributes shared by a number of games or chairs or leaves often helps us to learn how to employ the corresponding term, there is no set of characteristics that is simultaneously applicable to all members of the class and to them alone. Instead, confronted with a previously unobserved activity, we apply the term 'game' because what we are seeing bears a close 'family resemblance' to a number of the activities we have previously learned to call by that name. For Wittgenstein, in short, games, chairs, and leaves are natural families, each constituted by a network of overlapping and crisscross resemblances. The existence of such a network sufficiently accounts for our success in identifying the corresponding object or activity."– Thomas. Kuhn {The Structure of Scientific Revolutions}
To make the Similarity Network act more "complete," consider the following analogy. In a city, any person should be able to visit any other; but we do not build a special road between each pair of houses; we place a group of houses on a "block." We do not connect roads between each pair of blocks; but have them share streets. We do not connect each town to every other; but construct main routes, connecting the centers of larger groups. Within such an organization, each member has direct links to some other individuals at his own "level," mainly to nearby, highly similar ones; but each individual has also at least a few links to "distinguished" members of higher level groups. The result is that there is usually a rather short sequence between any two individuals, if one can but find it.
To locate something in such a structure, one uses a hierarchy like the one implicit in a mail address. Everyone knows something about the largest categories, in that he knows where the major cities are. An inhabitant of a city knows the nearby towns, and people in the towns know the nearby villages. No person knows all the individual routes between pairs of houses; but, for a particular friend, one may know a special route to his home in a nearby town that is better than going to the city and back. Directories factor the problem, basing paths on standard routes between major nodes in the network. Personal shortcuts can bypass major nodes and go straight between familiar locations. Although the standard routes are usually not quite the very best possible, our stratified transport and communication services connect everything together reasonably well, with comparatively few connections.
At each level, the aggregates usually have distinguished foci or capitols. These serve as elements for clustering at the next level of aggregation. There is no non-stop airplane service between New Haven and San Jose because it is more efficient overall to share the "trunk" route between New York and San Francisco, which are the capitols at that level of aggregation.
As our memory networks grow, we can expect similar aggregations of the destinations of our similarity pointers. Our decisions about what we consider to be primary or "trunk" difference features and which are considered subsidiary will have large effects on our abilities. Such decisions eventually accumulate to become epistemological commitments about the "conceptual" cities of our mental universe.
The non-random convergences and divergences of the similarity pointers, for each difference D, thus tend to structure our conceptual world around
(1) the aggregation into D-clusters
(2) the selection of D-capitols
Note that it is perfectly all right to have several capitols in a cluster, so that there need be no one attribute common to them all. The "crisscross resemblances" of Wittgenstein are then consequences of the local connections in our similarity network, which are surely adequate to explain how we can feel as though we know what is a chair or a game–yet cannot always define it in a "logical" way as an element in some class-hierarchy or by any other kind of compact, formal, declarative rule. The apparent coherence of the conceptual aggregates need not reflect explicit definitions, but can emerge from the success-directed sharpening of the difference-describing processes.
The selection of capitols corresponds to selecting stereotypes or typical elements whose default assignments are unusually useful. There are many forms of chairs, for example, and one should choose carefully the chair-description frames that are to be the major capitols of chair-land. These are used for rapid matching and assigning priorities to the various differences. The lower priority features of the cluster center then serve either as default properties of the chair types or, if more realism is required, as dispatch pointers to the local chair villages and towns.
Difference pointers could be "functional" as well as geometric. Thus, after rejecting a first try at "chair" one might try the functional idea of "something one can sit on" to explain an unconventional form. This requires a deeper analysis in terms of forces and strengths. Of course, that analysis would fail to capture toy chairs, or chairs of such ornamental delicacy that their actual use would be unthinkable. These would be better handled by the method of excuses, in which one would bypass the usual geometrical or functional explanations in favor of responding to contexts involving art or play.
It is important to re-emphasize that there is no reason to restrict the memory structure to a single hierarchy; the notions of "level" of aggregation need not coincide for different kinds of differences. The d-capitols can exist, not only by explicit declarations, but also implicitly by their focal locations in the structure defined by convergent d-pointers. (In the Newell-Simon GPS framework, the "differences" are ordered into a fixed hierarchy. By making the priorities depend on the goal, the same memories could be made to serve more purposes; the resulting problem-solver would lose the elegance of a single, simply-ordered measure of "progress," but that is the price of moving from a first-order theory.)
Finally, we should point out that we do not need to invoke any mysterious additional mechanism for creating the clustering structure. Developmentally, one would assume, the earliest frames would tend to become the capitols of their later relatives, unless this is firmly prevented by experience, because each time the use of one stereotype is reasonably successful, its centrality is reinforced by another pointer from somewhere else. Otherwise, the acquisition of new centers is in large measure forced upon us from the outside: by the words available in one's language; by the behavior of objects in one's environment; by what one is told by one's teachers, family, and general culture. Of course, at each step the structure of the previous structure dominates the acquisition of the later. But in any case such forms and clusters should emerge from the interactions between the world and almost any memory-using mechanism; it would require more explanation were they not found!
3.6 ANALOGIES AND ALTERNATIVE DESCRIPTIONS
The method sketched in I.3 resulted in an analogy between the "discrete" space of index values Z = (1,2,...) and the continuous state space O of the k-dimensional mechanical system... That this cannot be achieved without some violence to the formalism and to mathematics is not surprising. The spaces Z and O are really very different, and every attempt to relate the two must run into great difficulties.
What we do have, however, is not a relation of Z to O, but only a relation between the functions in these two spaces, i.e., between the sequences x1,x2,... which are the functions in Z, and the wave functions f(q1,...qk) which are the functions in O. These functions, furthermore, are the entities which enter most essentially into the problems of quantum mechanics."– von Neumann {1955}
We have discussed the use of different frames of the same system to describe the same situation in different ways: for change of position in vision and for change of emphasis in language. In the wolf and lamb episode, for example, two frames are used in a before-after situation pair. Sometimes, in "problem-solving" we use two or more descriptions in a more complex way to construct an analogy or to apply two radically different kinds of analysis to the same situation. For hard problems, one "problem space" is usually not enough! The context of the von Neumann quotation is a proof that the two early formulations of quantum mechanics, Heisenberg's matrix theory and Schrodinger's wave mechanics, could be seen as mathematically identical, when viewed from the frame of Hilbert Space. Here, two very different structural descriptions were shown to be very similar, but only by representing both of them from a third viewpoint.
But we do not have to look to mathematics for such examples; we find the same thing in this everyday scenario: Suppose your car battery runs down. You believe that there is an electricity shortage and blame the generator.
Seen as a mechanical system, the generator can be represented as a rotor with pulley wheel driven by a belt from the engine. Is the belt still intact and tight enough? The output, seen mechanically, is a cable to the battery. Is the cable still intact? Are the bolts tight, etc.?
Seen electrically, the generator's rotor is seen as a flux-linking coil. The brushes and commutator (in older models) are seen as electrical switches. The output is current that runs through conductors.
We thus represent the situation in two quite different frame-systems. In one, the armature is a mechanical rotor with pulley, in the other it is a conductor in a changing magnetic field. The same–or analogous–elements share terminals of different frames, and the frame-transformations apply only to some of them.
The differences between the two frames are substantial. The entire mechanical chassis of the car plays the simple role, in the electrical frame, of one of the battery connections. The diagnostician has to use both representations. A failure of current to flow often means that an intended conductor is not acting like one. For this case, the basic transformation between the frames depends on the fact that electrical continuity is in general equivalent to firm mechanical attachment. Therefore, any conduction disparity revealed by electrical measurements should make us look for a corresponding disparity in the mechanical frame. In fact, since "repair" in this universe is synonymous with "mechanical repair," the diagnosis must end in the mechanical frame. Eventually, we might locate a defective mechanical junction and discover a loose connection, corrosion, wear, or whatever.
Why have two separate frames, rather than one integrated structure to represent the generator? I believe that in such a complex problem one can never cope with many details at once. At each moment one must work within a reasonably simple framework. I contend that any problem that a person can solve at all is worked out at each moment in a small context and that the key operations in problem solving are concerned with finding or constructing these working environments.
Indeed, finding an electrical fault requires moving between at least three frames: a visual one along with the electrical and mechanical frames. If electrical evidence suggests a loose mechanical connection, one needs a visual frame to guide one's self to the mechanical fault.
Are there general methods for constructing adequate frames? The answer is both yes and no! There are some often-useful strategies for adapting old frames to new purposes; but I should emphasize that humans certainly have no magical way to solve all hard problems! One must not fall into what Papert calls the Superhuman-Human Fallacy and require a theory of human behavior to explain even things that people cannot really do!
One cannot expect to have a frame exactly right for any problem or expect always to be able to invent one. But we do have a good deal to work with, and it is important to remember the contribution of one's culture in assessing the complexity of problems people seem to solve. The experienced mechanic need not routinely invent; he already has engine representations in terms of ignition, lubrication, cooling, timing, fuel mixing, transmission, compression, and so forth. Cooling, for example, is already subdivided into fluid circulation, air flow, thermostasis, etc. Most "ordinary" problems are presumably solved by systematic use of the analogies provided by the transformations between pairs of these structures. The huge network of knowledge, acquired from school, books, apprenticeship, or whatever is interlinked by difference and relevancy pointers. No doubt the culture imparts a good deal of this structure by its conventional use of the same words in explanations of different views of a subject.
What about interactions that cross many of these boundaries? A Gestalt philosopher might demand some kind of synthesis in which one sees the engine as a whole. But before we demand a general solution, we should remind ourselves that for faults that stem from three-or-more interacting elements, a human auto mechanic will diagnose them, if at all, only after expensive, exhaustive replacement of many innocent components. Thus, the desire for complete synthesis should not be a theoretical requirement. To be sure, there must indeed be some structure linking together the different conceptual engine frames. But this, too, may be relatively simple. Perhaps one must add a fourth engine-super-frame whose terminals point to the various electrical, mechanical, and visual representation frames, and are themselves interconnected by pointers describing when and how the different subframes are to be used. Presumably every complicated system that is "understood" contains some super-frame structures that direct the utilization of subframes.
Incidentally, it is tempting in our culture to believe that a larger view is taken in our subconscious minds. As Poincare observes, one often comes upon a sudden illumination {Poincare, 1913} after a period of conscious formulation, followed by a much longer period of non-conscious activity. I read his further discussion as proposing that the unconscious activity is a combinatorial heuristic search in which the chance of success depends mainly of the quality of the ingredients introduced by the preliminary conscious analysis; these elements are combined in different ways until a configuration is reached that passes some sort of test.
"I have spoken of the feeling of absolute certitude accompanying the inspiration...; often this feeling deceives us without being any the less vivid, and we only find it out when we seek to put on foot the demonstrations. I have especially noticed this fact in regard to ideas coming to me in the morning or evening in bed while in a self-hypnagogic state."–H. Poincare {Foundations of Science}
The product of inspiration is thus not a fully detailed solution but a "point of departure" or plan, brought to consciousness because it has passed some sort of threshold of "esthetic sensibility."
On this last point Poincare does indeed seem to subscribe to a holistic conception for he characterizes "elegant" mathematical entities as those "whose elements are so harmoniously disposed that the mind can embrace their totality while realizing the details." It remains to be seen whether the filters that admit new descriptive combinations to the status of fully conscious attention require a complex, active analysis or can be explained by simpler matching and retrieval operations. (It is an unhappy fact that mathematicians have not contributed much to understanding the mechanisms of problem-solving–with the exception of Poincare, Polya, and a few others. I wonder if this is not largely due to their attachment to the concept of "elegance"–passed from one generation to the next as an intangible quality, worshipped but not explained or analyzed.) In any case, I see no reason to suppose that the unconscious is distinguished either along the dimension of massive parallel computation or by extraordinary holistic synthesis. A more plausible function would seem to be rapid, shallow exploration using material prepared by earlier analysis. The unconscious aspect might only reflect the lack of "annotation" and record-keeping that would make the process otherwise accessible to review and analysis. But the question about the complexity of the acceptance filter certainly still stands.
3.7 SUMMARIES: USING FRAMES IN HEURISTIC SEARCH
Over the past decade, it has become widely recognized how important are the details of the representation of a "problem space"; but it was not so well recognized that descriptions can be useful to a program, as well as to the person writing the program. Perhaps progress was actually retarded by ingenious schemes to avoid explicit manipulation of descriptions. Especially in "theorem-proving" and in "game-playing" the dominant paradigm of the past might be schematized so:
The central goal of a Theory of Problem Solving is to find systematic ways to reduce the extent of the Search through the Problem Space.
Sometimes a simple problem is indeed solved by trying a sequence of "methods" until one is found to work. Some harder problems are solved by a sequence of local improvements, by "hill-climbing" within the problem space. But even when this solves a particular problem, it tells us little about the problem-space; hence yielding no improved future competence. The best-developed technology of Heuristic Search is that of game-playing using tree-pruning, plausible-move generation, and terminal-evaluation methods. But even those systems that use hierarchies of symbolic goals do not improve their understanding or refine their representations. I now propose a more mature and powerful paradigm:
The primary purpose in problem solving should be better to understand the problem space, to find representations within which the problems are easier to solve. The purpose of search is to get information for this reformulation, not–as is usually assumed–to find solutions; once the space is adequately understood, solutions to problems will more easily be found.
In particular, I reject the idea that the value of an intellectual experiment should be assessed along the dimension of success - partial success - failure, or in terms of "improving the situation" or "reducing a difference." An application of a "method," or a reconfiguration of a representation can be valuable if it leads to a way to improve the strategy of subsequent trials. Earlier formulations of the role of heuristic search strategies did not emphasize these possibilities, although they are implicit in discussions of "planning."
How can the new paradigm be combined with the classical 'minimax' strategy? In a typical episode, one is located at a certain node A in the search tree, and examines two or more possible moves, say, B and C. Each of these is somehow evaluated to yield values V(B) and V(C). Then these are somehow combined to yield a score, S(A) = M(V(B), V(C)), where M is some function that takes two numbers and yields one. In effect, M has to summarize the results of all the search below A and compress them into a single numerical quantity to represent the value of being at node A.
Now, what is the purpose of this? If one were able to search the entire game-tree, we could use S at each node to decide which move is best to make. Since we cannot search the whole tree, we need information about what next to explore; we want S to tell the move generator what kinds of moves to consider. But if S is a mere number, this is unsuitable for much reasoning or analysis.
If S(B) has a low value, we can assume that B is a bad position. But if we want the move generator not to make the "same kind of mistake" again, the message must contain some additional clue about why B is weak–or better, what to do about it. So we really need a summary explanation of what was found in the search; and since we are in a tree we need further to summarize such summaries recursively.
There is a problem here we might call "summary-divergence." If the summary of the situation at A contains (in general) any explicit mention of B and C, then any recursive description scheme is in danger of containing an explicit copy of the entire move-tree; then to answer a question one might have nearly as bad a time searching the summary as the game-tree itself. One way to prevent this is simply to limit the size of the summary. However, we can avoid such drastic knowledge-destruction; in a frame-description, the important features and relations at the top levels can serve as summaries while the lower-level subsidiary descriptions can be accessed only if necessary. How much of the whole analysis tree remains in long term memory, and how much is left as garbage after the move is made would depend on other aspects of how the game-player uses his general experience.
How are the summaries to be made? Again, the frame idea suggests a flexible approach. Instead of demanding a rigid format, we could build up a collection of ad hoc "summary" frames, each evoked when their terminals fit subordinate descriptions and its frame-markers match the current goals. Thus each does its job when appropriate. For example, one might have a variety of "fork" frames. If a Knight lands on a square that threatens both check and rook capture, a fork frame is activated by its condition that in each of only two plausible moves, the unmoved piece is lost. Once this frame is activated it can make a specific recommendation, perhaps that the generator for the forked player see if a previously available move can apply additional defense to the forking square.
3.8 FRAMES AS PARADIGMS
"Until that scholastic paradigm the medieval 'impetus' theory was invented, there were no pendulums, but only swinging stones, for scientists to see. Pendulums were brought into the world by something very like a paradigm-induced gestalt switch. Do we, however, really need to describe what separates Galileo from Aristotle, or Lavoisier from Priestly, as a transformation of vision? Did these men really see different things when looking at the same sorts of objects? Is there any legitimate sense in which we can say they pursued their research in different worlds?
{I am} acutely aware of the difficulties created by saying that when Aristotle and Galileo looked at swinging stones, the first saw constrained fall, the second a pendulum. Nevertheless, I am convinced that we must learn to make sense of sentences that at least resemble these."–T. Kuhn {The Structure of Scientific Revolutions}
According to Kuhn's model of scientific evolution "normal" science proceeds by using established descriptive schemes. Major changes result from new "paradigms," new ways of describing things that lead to new methods and techniques. Eventually there is a redefining of "normal."
Now while Kuhn prefers to apply his own very effective re-description paradigm at the level of major scientific revolutions, it seems to me that the same idea applies as well to the microcosm of everyday thinking. Indeed, in that last sentence quoted, we see that Kuhn is seriously considering the paradigms to play a substantive rather than metaphorical role in visual perception, just as we have proposed for frames.
Whenever our customary viewpoints do not work well, whenever we fail to find effective frame systems in memory, we must construct new ones that bring out the right features. Presumably, the most usual way to do this is to build some sort of pair-system from two or more old ones and then edit or debug it to suit the circumstances. How might this be done? It is tempting to formulate it in terms of constructing a frame-system with certain properties. This appears to simplify the problem by dividing it into two stages: first formulate the requirements, and then solve the construction problem.
But that is certainly not the usual course of ordinary thinking! Neither are requirements formulated all at once, nor is the new system constructed entirely by deliberate pre-planning. Instead we recognize unsatisfied requirements, one by one, as deficiencies or "bugs," in the course of a sequence of modifications made to an unsatisfactory representation.
I think (Papert, 1972) is correct in believing that the ability to diagnose and modify one's own procedures is a collection of specific and important "skills." Debugging, a fundamentally important component of intelligence, has its own special techniques and procedures. Every normal person is pretty good at them; or otherwise he would not have learned to see and talk! Although this essay is already speculative, I would like to point here to the theses of Goldstein (1974) and Sussman (1973) about the explicit use of knowledge about debugging in learning symbolic representations. They build new procedures to satisfy multiple requirements by such elementary but powerful techniques as:
•Make a crude first attempt by the first order method of simply putting together procedures that separately achieve the individual goals.
•If something goes wrong, try to characterize one of the defects as a specific (and undesirable) kind of interaction between two procedures.
•Apply a "debugging technique" that, according to a record in memory, is good at repairing that specific kind of interaction.
•Summarize the experience, to add to the "debugging techniques library" in memory.
These might seem simple-minded, but if the new problem is not too radically different from the old ones, then they have a good chance to work, especially if one picks out the right first-order approximations. If the new problem is radically different, one should not expect any learning theory to work well. Without a structured cognitive map–without the "near misses" of Winston, or a cultural supply of good training sequences of problems–we should not expect radically new paradigms to appear magically whenever we need them.
What are "kinds of interactions," and what are "debugging techniques?" The simplest, perhaps, are those in which the result of achieving a first goal interferes with some condition prerequisite for achieving a second goal. The simplest repair is to reinsert that prerequisite as a new condition. There are examples in which this technique alone cannot succeed because a prerequisite for the second goal is incompatible with the first. Sussman presents a more sophisticated diagnosis and repair method that recognizes this and exchanges the order of the goals. Goldstein considers related problems in a multiple description context.
If asked about important future lines of research on Artificial or Natural Intelligence, I would point to the interactions between these ideas and the problems of using multiple representations to deal with the same situation from several viewpoints. To carry out such a study, we need better ideas about interactions among the transformed relationships. Here the frame-system idea by itself begins to show limitations. Fitting together new representations from parts of old ones is clearly a complex process itself, and one that could be solved within the framework of our theory (if at all) only by an intricate bootstrapping. This, too, is surely a special skill with its own techniques. I consider it a crucial component of a theory of intelligence.
We must not expect complete success in the above enterprise; there is a difficulty, as Newell (1973) notes in a larger context:
"'Elsewhere' is another view–possibly from philosophy–or other 'elsewheres' as well, since the views of man are multiple. Each view has its own questions. Separate views speak mostly past each other. Occasionally, of course, they speak to the same issue and then comparison is possible, but not often and not on demand."
4 CONTROL
I have said little about the processes that manipulate frame-systems. This is not the place to discuss long-duration management of thought involving such problems as controlling a large variety of types of goals, sharing time between chronic and acute concerns, or regulating allocation of energy, storage, and other resources.
Over much smaller time spans–call them episodes–I imagine that thinking and understanding, be it perceptual or problem-solving, is usually concerned with finding and instantiating a frame. This breaks large problems down into many small jobs to be done and raises all the usual issues about heuristic programming, the following for example:
TOP-DOWN OR LATERAL: Should one make a pass over all the terminals first, or should one attempt a complete, detailed instantiation of some supposedly most critical one? In fact, neither policy is uniformly good. One should usually "look before leaping," but there must be pathways through which an interesting or unexpected event can invoke a subframe to be processed immediately.
CENTRAL CONTROL: Should a frame, once activated, "take over" and control its instantiation, or should a central process organize the operation. Again, no uniform strategy is entirely adequate. No "demon" or other local process can know enough about the overall situation to make good decisions; but no top-level manager can know enough details either.
Perhaps both issues can be resolved by something involving the idea of "back-off" proposed to me by William Martin in contrast to "back-up" as a strategy for dealing with errors and failures. One cannot either
release control to subsidiaries or keep it at the top, so we need some sort of interpreter that has access both to the top level goals and to the operation of the separate "demons." In any case, one cannot ask for a uniform strategy; different kinds of terminals require different kinds of processes. Instantiating a wall terminal of a room-frame invites finding and filling a lower level wall subframe, while instantiating a door terminal invites attaching another room frame to the house frame. To embed in each frame expectations about such matters, each terminal could point to instructions for the interpreter about how to collect the information it needs and how to complain about difficulties or surprises.
In any case, the frame-filling process ought to combine at least the components of decision-tree and demon-activation processes: in a decision tree, control depends on results of tests. A particular room frame, once accepted, might test for a major feature of a wall. Such tests would work through a tree of possible wall frames, the tree structure providing a convenient non-linear ordering for deciding which default assignments can remain and which need attention.
In a demon model, several terminals of an evoked frame activate "demons" for noticing things. A round object high on a center wall (or elliptical on a side wall) suggests a clock, to be confirmed by finding an appropriate number, mark, or radial line.
If not so confirmed, the viewer would have "seen" the clock but would be unable to describe it in detail. An eye-level trapezoid could indicate a picture or a window; here further analysis is usually mandatory.
The goal of Seeing is not a fixed requirement to find what is out there in the world; it is subordinate to answering questions by combining exterior visual evidence with expectations generated by internal processes. Nevertheless, most questions require us in any case to know our orientation with respect to our immediate surroundings. Therefore a certain amount of "default" processing can proceed without any special question or goal. We clearly need a compromise in which a weak default ordering of terminals to be filled is easily superseded when any demon encounters a surprise.
In the "productions" of Newell and Simon (1972), the control structure is implicit in the sequential arrangement (in some memory) of the local behavior statements. In systems like the CONNIVER language there are explicit higher-level control structures {McDermott and Sussman, 1972}, but a lot still depends on which production-like assertions are currently in active memory and this control is not explicit. Both systems feature a high degree of local procedural control. Anything "noticed" is matched to an "antecedent pattern" which evokes another subframe, attaches it, and executes some of its processes.
There remains a problem. Processes common to many systems ought to be centralized, both for economy and for sharing improvements that result from debugging. Too much autonomy makes it hard for the whole system to be properly responsive to central, high level goals. The next section proposes one way such conflicts might possibly be resolved. A frame is envisioned as a "packet" of data and processes and so are the high level goals. When a frame is proposed, its packet is added to the current program "environment" so that its processes have direct access to what they need to know, without being choked by access to the entire knowledge of the whole system. It remains to be seen how to fill in the details of this scheme and how well it will work.
I should explain at this point that this manuscript took shape, over more than a year, in the form of a file in the experimental ARPA computer network–the manuscript resided at various times in two different MIT computers and one at Stanford, freely accessible to students and colleagues. A graduate student, Scott Fahlman, read an early draft before it contained a control scheme. Later, as part of a thesis proposal, Fahlman presented a control plan that seemed substantially better than my own, which he had not seen, and the next section is taken from his proposal. Several terms are used differently, but this should cause no problem.
The following essay was written by Scott Fahlman (in 1974 or 1973?), when a student at MIT. It is still one of the clearest images of how societies of mind might work. I have changed only a few terms. Fahlman, now a professor at Carnegie-Mellon University, envisioned a frame as a packet of related facts and agencies–which can include other frames. Any number of frames can be aroused at once, whereupon all their items–and all the items in their sub-frames as well–become available unless specifically canceled. The essay is about deciding when to allow such fragments of information to become active enough to initiate yet other processes.
Frame Verification (by Scott Fahlman
"I envision a data base in which related sets of facts and demons are grouped into packets, any number of which can be activated or made available for access at once. A packet can contain any number of other packets (recursively), in the sense that if the containing packet is activated, the contained packets are activated as well, and any data items in them become available unless they are specifically modified or canceled. Thus, by activating a few appropriate packets, the system can create a tailor-made execution environment containing only the relevant portion of its global knowledge and an appropriate set of demons. Sometimes, of course, it will have to add specific new packets to the active set in order to deal with some special situation, but this inconvenience will be far less than the burden of constantly tripping over unwanted knowledge or triggering spurious demons.
"The frame begins the verification process by checking any sample features that it already has on hand - features that arrived in the first wave or were obtained while testing previous hypotheses. Then, if the hypothesis has not already been accepted or rejected, the frame begins asking questions to get more information about features of the sample. The nature of these questions will vary according to the problem domain: A doctor program might order some lab tests, a vision program might direct its low-level components to look at some area more closely. Sometimes a question will recursively start another recognition process: 'This might be a cow–see if that part is an udder.'
"The order in which the questions are asked is determined by auxiliary information in the frame. This information indicates which features are the most critical in the verification at hand, how these priorities might be affected by information already present, and how much each question will cost to answer. As each new feature of the sample is established, its description is added to a special packet of information about the sample, along with some indication of where the information came from and how reliable it is. This packet can be taken along if the system moves to another hypothesis. Sometimes unsolicited information will be noticed along the way; it, too, is tested and thrown into the pot.
"Of course, the system will practically never get a perfect match to any of its ideal exemplars. Auxiliary frame information will indicate for each expected type of violation whether it should be considered trivial, serious, or fatal (in the sense that it decisively rules out the current frame). Continuously variable features such as size, body proportions, or blood pressure will have a range of normal variation indicated, along with a mapping from other ranges into seriousness values. Sometimes a feature will provide no real evidence for or against a hypothesis, but can be explained by it; this, too, is noted in the frame. If there are striking or conspicuous features in the sample (antlers, perhaps) that are not mentioned in the current frame, the system will usually consider these to be serious violations; such features are evaluated according to information stored in a packet associated with the feature, since the hypothesis frame clearly cannot mention every feature not present in the exemplar.
"Occasionally a feature will have a strong confirming effect: If you see it, you can stop worrying about whether you are in the right place. Usually, though, we will not be so lucky as to have a decisive test. The normal procedure, then, is to gather in sample features until either some satisfaction level is reached and the hypothesis is accepted, or until a clear violation or the weight of several minor violations sends the system off in search of something better. (My current image of the satisfaction level is as some sort of numerical score, with each matched feature adding a few points and each trivial mismatch removing a few. Perhaps some more complex symbolic scheme will be needed for this, but right now I do not see why.) The satisfaction level can vary considerably, according to the situation: The most cursory glance will convince me that my desk is still in my office, while a unicorn or a thousand dollar bill will rate a very close inspection before being accepted.
"Sometimes the sample will appear to fit quite well into some category, but there will be one or two serious violations. In such a case the system will consider possible excuses for the discrepancies: Perhaps the cow is purple because someone has painted it. Perhaps the patient doesn't have the expected high blood pressure because he is taking some drug to suppress it. If a discrepancy can be satisfactorily explained away, the system can accept the hypothesis after all. Of course, if the discrepancies suggest some other hypothesis, the system will try that first and resort to excuses only if the new hypothesis is no better. Sometimes two categories will be so close together that they can only be told apart by some special test or by paying particular attention to some otherwise insignificant detail. It is a simple enough matter for both of the frames to include a warning of the similarity and a set of instructions for making the discrimination. In medicine, such testing is called differential diagnosis.
"Note that this use of exemplars gives the system an immense flexibility in dealing with noisy, confused, and unanticipated situations. A cow may formally be a large quadruped, but our system would have little trouble dealing with a three-legged cow amputee, as long as it is a reasonably good cow in most other respects. (A missing leg is easy to explain; an extra one is somewhat more difficult.) If the system is shown something that fits none of its present categories, it can at least indicate what the sample is close to, along with some indication of the major deviations from that category. A visual system organized along these lines might easily come up with 'like a person, only 80 feet tall and green' or 'a woman from the waist up and a tuna fish from the waist down.' Under certain circumstances, such descriptions might serve as the nuclei of new recognition frames representing legitimate, though unnamed, conceptual categories.
"An important feature of recognition frames (and of the recognition categories they represent) is that they can be organized into hierarchies. The system can thus hypothesize at many levels, from the very general to the very specific: An animal of some sort, a medium-sized quadruped, a dog, a collie, Lassie. Each level has its own recognition frame, but the frames of the more specific hypotheses include the information packets of the more general frames above them; thus, if the system is working under the 'dog' frame, the information in the 'animal' frame is available as well. A specific frame may, of course, indicate exceptions to the more general information: The 'platypus' frame would include the information in 'mammal', but it would have to cancel the parts about live birth of young. Often a general frame will use one of the specific cases below it as its exemplar; 'mammal' might simply use 'dog' or 'cow' as its exemplar, rather than trying to come up with some schematic model of an ideal non-specific mammal. In such a case, the only difference between hypothesizing 'mammal' and 'cow' would be a somewhat greater reluctance to move to another mammal in the latter case; the system would test the same things in either case.
"Note that there can be many different hierarchical networks, and that these can overlap and tangle together in interesting ways: A komodo dragon is taxonomically a reptile, but its four-legged shape and its habits are closer to a dog's than to a snake's. How to represent these entanglements and what to do about them are problems that will require some further thought. Some frames are parasitic: Their sole purpose is to attach themselves to other frames and alter the effects of those frames. (Perhaps 'viral' would be a better term.) 'Statue-of' might attach to a frame like 'cow' to wipe out its animal properties of motion and material (beef), while leaving its shape properties intact. 'Mythical' could be added to animal to make flying, disappearance, and the speaking of riddles in Latin more plausible, but actual physical presence less so. Complications could be grafted onto a disease using this mechanism. There is nothing to prevent more than one parasite at a time from attaching to a frame, as long as the parasites are not hopelessly contradictory; one could, for instance, have a statue of a mythical animal.
5 SPATIAL IMAGERY
5.1 Places and headings. Merits of global frame for familiar complex objects.
We normally imagine ourselves moving within a stationary spatial setting. The world does not recede when we advance; it does not spin when we turn! At my desk I am aware of a nearby river whose direction I think of as north although I know that this is off by many degrees, assimilated years ago from a truer north at another location on the same river. This sense of direction permeates the setting; the same "north" is constant through one's house and neighborhood, and every fixed object has a definite heading .
Besides a heading, every object has a place . We are less positive about the relations between places from one room to another. This is partly because heading is computationally simpler but also because (in rectangular rooms) headings transfer directly whereas "place" requires metric calculations.
In unfamiliar surroundings, some persons deal much less capriciously than others with headings. One person I know regularly and accurately relates himself to true compass direction. He is never lost in a new city. Only a small part of this is based on better quantitative integration of rotations. He uses a variety of cues–maps, shadows, time-of-day, major landmarks (even glimpsed from windows), and so forth. It seems at first uncanny, but it doesn't really require much information. The trick is to acquire effective habits of noticing and representing such things.
Once acquired, headings are quite persistent and are difficult to revise when one tries to make "basic" changes. When I finally understood the bend in the river, it did not seem worth the effort to rebuild my wrong, large-scale spatial model. Similarly, I spent years in Boston before noticing that its "Central Park" has five sides. A native of rectangular Manhattan, I never repaired the thoroughly non-Euclidean nonsense this mistake created; there is simply no angular sector space in it to represent Boston's North End.
Such difficulties suggest that we use gross, global frames of reference as well as smaller, local structures. The difficulty of rearrangement suggests that the local frames are not complete, transformable, structures but depend on their attachment to "global frames" to deduce inter-object relationships. Below I discuss some implications of using global reference systems; in principle this suggests more powerful and general processes for rearranging parts of complicated images, but in practice people seem quite limited at this, especially when operating under time constraints.
5.2 A GLOBAL SPACE FRAME SYSTEM?
I do not like the following model very much, but something of its sort seems needed. A Global Space Frame –(GSF for short) –is a fixed collection of "typical locations" in an abstract three dimensional space, and copies of it are used as frameworks for assembling components of complex scenes. One might imagine such a skeleton as a five-by-five horizontal array of "places," each with three vertical levels. The central cells represent zones near the center of interest, while the peripheral cells have to represent everything else.
Then instead of using two-dimensional appearances, one might use cells which correspond to places one can reach. A room is framed as a three-by-three-by-three array of cubic cells like this:
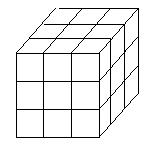
In effect, one always imagines oneself within this universal ghost-room in which one's current real environment is also embedded. More likely, people use skeletons more complicated and less mathematically regular than this, emphasizing easily-accessible volumes near the hands and face to represent space in ways more directly related to manipulative access.
The GSF is associated with a system of view-frames; each view-frame describes the visual appearance of the GSF from a different observer viewpoint. The system is thus both Copernican and Ptolemaic; the embedding of the current scene in the GSF skeleton does not change when the observer moves, but each viewpoint gives the scene a distinctive appearance because the observer's location (or, rather, his belief about his location) activates an appropriate view-frame.
The view-frame corresponding to any particular place is derived by projecting the GSF cells toward that place; this yields an array of view-lists–each of which is an ordered list of those cells of the GSF that would intersect some certain ray emitted from the observer's eye. Thus a view-frame is like an ordinary scene frame except that its elements are derived from the GSF skeleton rather than from specific visual features and relations of any particular scene. While view-lists correspond to retinal regions, we think of them as three-dimensional zones extending in some general direction out to distant space.
Occlusions are explained or imagined in terms of view-list orderings; one expects not to see all of an object that comes later on a view-list than does another object. (Similarly, earlier objects are obstacles to manipulating later ones.) In memory matching, occluded view-list cells should relax the matching constraints on corresponding terminals.
To absorb visual information from multiple viewpoints, we need some sort of "indirect-address" scheme in which visual features are assigned to view-frames through the GSF skeleton; here is a first-order sketch of such a scheme:
SEEING: A variety of types of visual "features" are detected by retinal or post-retinal "feature-demons." Each detected feature is automatically associated with the view-direction of the current view-list corresponding to its location in the visual field.
FRAME-ACTIVATION: At the same moment, some object-frame or expectation is tentatively assigned to some of the GSF cells in the current view-list for that direction. This means that each terminal of that frame is associated with the view-direction of some active view-list. (In other words, scene frame terminals contain spatial-location information by pointing to GSF places. See below.) Different scene frames of the same system are selected according to the current view-frame. The headings of objects must be appropriately transformed.
INSTANTIATION: When looking in a certain direction we (a) expect to see certain visual features in certain cells, as suggested by the active scene frame and (b) we actually see certain features in certain visual regions. So it is natural to propose a first-order vision theory in which each marker of each terminal actually specifies the signature–and also the proposed GSF location-cell–of some class of visual feature-demon. The observer can also be represented within the system as an object, allowing one to imagine himself within a scene but viewed from another location.
Given all this it is easy to obtain the information needed to assign terminals and instantiate frames. All the system has to do is match the "perceptual" {feature-demon, view-list} pairs to the "schematic" {marker, GSF-cell} pairs. If object-frame terminals could be attached directly to GSF locations and if these were automatically projected into view-lists, this would eliminate almost all need to recompute representations of things that have already been seen from other viewpoints.
5.3 EMBEDDING COMPLICATIONS
In our first formulation, the terminals of a vision frame were understood to be in some way associated with cells of the GSF skeleton. The idea is tempting: why not abandon the whole visual frame-system idea and build "3-D" object-frames that map directly into space locations? Then an object-frame could represent almost directly a symbolic three-dimensional structure and the GSF system could automatically generate different view-frames for the object.
For a computer system, this might work very well. For a psychological model, it leaves too many serious problems: how can we deal with translations, rotations and scale-changes; how do we reorient substructures? A crude solution, for rotations, is to have for each object a few standard views–embeddings of different sizes and orientations. Before rejecting this outright, note that it might be entirely adequate for some kinds of performance and for early stages of development of others.
But in "adult" imagery, any object type can be embedded in so many different ways that some more general kind of transformation-based operation seems needed. The obvious mathematical solution, for purposes of relocation and scaling, is to provide some kind of intermediate structure: each object-frame could be embedded in a relocatable, "portable" mini-GSF that can be rotated and attached to any global GSF cell, with an appropriate "view-note" specifying how the prototype figure was transformed.
Providing such a structure entails more than merely complicating the embedding operation. It also requires building a "uniform structure" into the GSF, straightening out the early, useful, but idiosyncratic exaggerations of the more familiar parts of near-body space. Attractive as such a model might be, I simply do not believe one is ever actually realized in people. People are not very good at imagining transformed scenes; I quoted Hogarth's account of the very special training required, and I noted Piaget's observation that even moderate competence in such matters seems not to mature before the second decade.
We thus have a continuum of spatial mechanism theories to consider. I will not pick any particular point in this spectrum to designate as "the theory." This is not entirely because of laziness; it is important to recognize that each individual probably has to develop through some sequence of more-and-more sophisticated mechanisms. Before we can expect to build a theory consistent with developmental phenomena, we will have to understand better which mechanisms can suffice for different levels of image-manipulation performance. And we certainly need to see a much more complete psychological portrait of what people really do with spatial-visual imagery.
Some readers may ask: since we have come so close to building a three-dimensional analogue mechanism, why not simply do that in some more elegant and systematic way? Although this is a popular proposal, no one has moved past the early, inadequate Gestalt models to suggest how a practical scheme of this sort might function. The neuronal construction of a non-symbolic three-dimensional representation system is imaginable, but the problems of constructing hypothetical solids and surfaces within it bring us right back to the same computationally non-trivial –and basically symbolic–issues. And the equivalent of the instantiated view-list has to be constructed in any case, so far as I can see, so that the function of an intermediate, analogue space-model remains somewhat questionable.
5.4 EVOLUTION
Our frame theory assumes a variety of special mechanisms for vision and symbolic manipulation. I doubt that much of this arises from "self-organizing" processes; most of it probably depends on innately provided "hardware." What evolutionary steps could have produced this equipment? The arguments below suggest that the requirements of three-dimensional vision may have helped the evolution of frame-like representations in general.
In the early steps of visual evolution, the most critical steps must have concerned the refinement of specific feature-detectors for use in nutrition, reproduction, and defense. As both vision and mobility grew more sophisticated, it became more important to better relate the things that are seen to their places in the outer world–to locations that one can reach or leap at. Especially, one needs the transformations that compensate for postural changes. These problems become acute in competitive, motion-rich situations. In predation or flight, there is an advantage in being able to coordinate information obtained during motion; even if vision is still based on the simplest feature-list recognition scheme, there is an advantage in correct aggregation of different features seen at different times .
Many useful "recognition" schemes can be based on simple, linear, horizontal ordering of visual features. One can get even more by using similar data from two motion-related views, or by using changes (motion parallax) in a moving view. Since so much can be done with such lists, we should look (1) for recognition schemes based on matching linear memory frames to parts of such ordered sets and (2) for aggregation schemes that might serve as early stages in developing a coarse ground-plan representation. One would not expect anything like a ground plan at first; initially one would expect an egocentric polar representation, relating pairs of objects, or relating an object to some reference direction such as the sun. We would not expect relational descriptions, sophisticated figure-ground mechanisms, or three-dimensional schemata at early stages. (I know of no good evidence that animals other than men ever develop realistic ground plans; although other animals' behavior can appear to use them, there may be simpler explanations).
The construction and use of a ground plan requires evolution of the very same motion transformations needed to assign multiple view data to appropriate cells. For a theory of how these in turn might develop we need to imagine possible developmental sequences, beginning in egocentric angular space, that at every stage offer advantages in visual-motor performance.
Among such schemata, I would expect to find some structures that would also help to realize multiple memory frames with common terminals–since this is a similar (and simpler) problem. Other visual memory needs demand ways to file assignment sets in long term memory; one wants representations of one's home, nesting area, predation regions, mate, enemies, and "bad places." It would be of value to develop a reliable global orientation within one's territory, if one is that kind of animal.
While the needs of vision point toward frame-like symbol manipulation, they do not so clearly point toward processes in which one makes hypothetical internal substitutions, i.e., imagination. But those operations would be useful in any problem-solving activity that requires planning.
We should consider individual as well as evolutionary development. In an "adult" system one's current view-frame depends on where one thinks his feet are; and this requires accumulating rotations due to body posture, head rotation, and eye-direction. It would be no surprise to find "innate" hardware, perhaps in the frontal visual cortex, through which such postural parameters operate to re-address the signatures of visual feature-demons; the innateness hypothesis is supported by the good visual-motor coordination seen in the early infancy of many vertebrates. On the other hand, men could do with less pre-programming, given enough other mechanism to make this evolution within the individual reasonably certain.
Although the "adult" system is Copernican we would expect to find, in babies, more self-centered schemata. Perhaps the infant begins with a system centered around the face (rather than the feet), whose primary function is to relate vision to arm-motions; next one would expect a crude locomotor body image; only much later emerges the global system with a "permanent" sense of heading and within which the "observer" can freely move. This evolution from head through body to space-centered imagery would certainly be very laborious, but the infant has plenty of time. Perhaps one could study such a process, in microcosm, by seeing how people acquire the skill required for map-navigation. At first, one has to align the map with the scene; later this seems less necessary. The trick seems to involve representing both the scene and the map, alike, with respect to an internally defined reference direction for (say) North. Of course, part of this new skill involves improving one's collection of perspective transforms for irregular shapes of landmarks as one's viewpoint moves through extremes of obliquity.
In any case, the question is not to decide between "innate" and "developmental" models but to construct better scenarios of how intermediate systems would operate. the relative helplessness of the infant human does not mean he lacks the innate spatiomotor machinery of the infant horse, but perhaps only that its availability is "purposefully" delayed until the imagery prerequisites are also available for building the more complex system.
5.5 METRIC AND QUANTITATIVE ISSUES
Most people in our culture feel a conflict between (a) explaining thinking in terms of discrete symbolic descriptions and (b) the popular phenomenology in which the inner world seems continuously colored by magnitudes, intensities, strengths and weaknesses– entities with the properties of continua. Introspection or intuition is not very helpful in this area. I am convinced that the symbolic models are the more profound ones and that, perhaps paradoxically to some readers, continuous structures are restrictive and confining. We already illustrated this point in the discussion of evaluation functions in chess. To be sure, continuous variables (and "analogue machinery") could be helpful in many applications. There would be no basic problem in adding magnitudes, probabilities, utility theories, or comparable mathematical gadgets. On the other side, naive analysts underrate the power of symbolic systems. Perhaps we tend to reject the idea of symbolic descriptions because of our sense of "continuous awareness"–would we not notice any hypothetical processes in which one symbolic description is abruptly dissolved and replaced by another?
There would be no actual power in such a continuous awareness; for only a process that can reflect on what it has done–that can examine a record of what has happened–can have any consequences. Just as our ability to debug a computer program depends on the character and quality of traces and records, self-consciousness itself must depend on the quality and character of one's summaries of his own recent states. The "phenomenological" smoothness or roughness of a sequence of mental states would then reflect only the style of description used in the representation of that sequence.
In a computer-based robot, one certainly could use metric parameters to make exact perspective calculations. But in a theory of human vision, I think we should try to find out how well our image abilities can be simulated by "qualitative," symbolic methods. People are very poor at handling magnitudes or intensities on any absolute scale; they cannot reliably classify size, loudness, pitch, weight, into even so many as ten reliably distinct categories. In comparative judgements, too, many conclusions that might seem to require numerical information are already implied by simple order, or gross order of magnitude. Consider three objects A B C tentatively assigned, in that order, to a center wall of a room. If we move right and now find B to the left of A, we can reassign B to the foreground. There is even more information in crude judgements of apparent movement, which can be interpreted as (inverse) order of distance from the observer's line of motion.
One thus hardly ever needs quantitative precision; differential measurements are fine for nearby objects while correspondingly gross judgements suffice for objects at grossly different ranges. For most practical purposes it is enough to notice just a few relations between an object and its neighbors. The number of noticed relations need not even grow faster than the number of objects: if two objects are near opposite walls, then this fact is directly represented in the top-level room frame, and one rarely needs to know more; if two objects are close together, there is usually a smaller frame including both, which gives more information about their relation. So we would (correctly) expect people to find it hard to recall spatial relations between objects in distinct frames because reconstruction through chaining of several frames needs information that is not usually stored–and would be tedious and inaccurate in any case.
There are some substantial objections to the GSF scheme. It is in the nature of perspective that each nearby cell will occlude a number of far away cells, and the cell-boundary occlusions are so irregular that one would not be able to tell just which parts of a far away object will be occluded. (So the view-list idea does not work very well, but so far as human imagery is concerned, people have similar problems.) To improve the predictive quality of the system, the view-lists could be elaborated to view-structures for representing spatial relations more complex than simple "nearer-further." The metrical quality of the system could be dramatically improved, I think, by using "symbolic interpolation": consider together or sequentially two or more view-lists from nearby locations, and compromise between predictions that do not agree. One can thus better estimate the exact boundary of an occlusion by finding out which motions would make it certainly occur.
This idea of interpolation–or, in its simplest form, superposition–may often offer a way to improve the accuracy of an otherwise adequate strategy. If one averages–or otherwise summarizes–the predictions of two or more standard views, one obtains predictions of intermediate views that are better than one might imagine. Thus the calculations for body-image management (which one might suppose require complex vector and matrix transformations) might very well be handled by summing the expectations or predictions from the nearest "stereotype postures"–provided that the latter are reasonably adequate by themselves. It is tempting to generalize this to abstract activities, e.g., processes that can make symbolic use of multiple representations.
Another area in which quantitative methods seem important, at least on the surface, is in memory retrieval. One needs mechanisms for controlling the allowed range-of-variation of assignments. Does one demand "best match," does one require a threshold of fit, or what? No one policy will work well. Consider a request of the form
"Pick up the big red block."
To decide what is "biggest," one has to compare different dimensions. Rather than assign a fixed procedure–which might work in simple problems–one should refer to the current problem-goal. If one is concerned with weight, then biggest = heaviest should work. If one is propping up a window, then biggest = largest dimension–that is, longest–is appropriate. The situation is more complex with unspecified selection, as in
"Pick up a big red block."
but the same principles apply: divide the world into classes appropriate to the micro-world we are in and then pick one from that class that best fits "big." Normally "big" means biggest, but not in a context that refers also to "enormous" blocks. Again, one must choose from one's collection of clustering methods by using the goal - microworld context. But here, again, the quantitative aspects should be on tap, not on top, or else the outstandingly important aspects of each domain will not be captured. McDermott (1973) discusses many issues about discrete representation of spatial structures in his thesis.
This essay contains quite a few different arguments against quantitative models. Perhaps I should explain the general principle upon which they are based, since I see that separately they are not very compelling. Thesis: the output of a quantitative mechanism, be it numerical, statistical, analogue, or physical (non-symbolic), is too structureless and uninformative to permit further analysis. Number-like magnitudes can form the basis of decisions for immediate action, for muscular superpositions, for filtering and summing of stimulus features, and so forth. But each is a "dead end" so far as further understanding and planning is concerned, for each is an evaluation–and not a summary.
A Number cannot reflect the considerations that formed it.
Thus, although quantitative results are useful for immediate purposes, they impose a large cost on further and deeper development.
This does not mean that people do not, or even that they should not, use such methods. But because of the block they present to further contemplation, we can predict that they will tend to be focused in what we might call terminal activities. In large measure, these may be just the activities most easily seen behavioristically and this might account in part for the traditional attraction of such models to workers in the behavioristic tradition. The danger is that theories based upon them–response probabilities, subjective probabilities, reinforcement schedule parameters–are not likely to be able to account for sophisticated cognitive activities. As psychological theories they are very likely to be wrong.
At times I may have overemphasized ways in which other kinds of first-order models can be satisfactory. This may be an over-reaction to some holism-oriented critics who showed (but did not notice) that if you can always notice one more feature of a situation, then you can make yourself believe that you have already noticed an infinite number of them. On the other side I may have overreacted against colleagues who ignore introspective phenomenology too thoroughly, or try to explain behavior in terms of unstructured elementary fragments. While any theory must "reduce" things to simpler elements, these need not be identifiable with behaviorally observable units of learning or doing.
6 Criticism of the Logistic Approach
"If one tries to describe processes of genuine thinking in terms of formal traditional logic, the result is often unsatisfactory; one has, then, a series of correct operations, but the sense of the process and what was vital, forceful, creative in it seems somehow to have evaporated in the formulations." –Max Wertheimer in {Productive Thinking}
I here explain why I think that more "logical" approaches will not work. There have been serious attempts, from as far back as Aristotle, to represent common sense reasoning by a "logistic" system–that is, one that makes a complete separation between
(1) "Propositions" that embody specific information, and
(2) "Syllogisms" or general laws of proper inference.
No one has been able successfully to confront such a system with a realistically large set of propositions. I think such attempts will continue to fail, because of the character of logistic in general rather than from defects of particular formalisms. (Most recent attempts have used variants of "first order predicate logic," but I do not think that is the problem.)
A typical attempt to simulate common-sense-thinking by logistic systems begins in a "microworld" of limited complication. At one end are high-level goals such as "I want to get from my house to the Airport." At the other end we start with many small items–the axioms–like "the car is in the garage," "one does not go outside undressed," "to get to a place one should (on the whole) move in its direction," etc. To make the system work one designs heuristic search procedures to "prove" the desired goal, or to produce a list of actions that will achieve it.
I will not recount the history of attempts to make both ends meet–but merely summarize my impression: in simple cases one can get such systems to "perform," but as we approach reality the obstacles become overwhelming. The problem of finding suitable axioms–the problem of "stating the facts" in terms of always-correct, logical, assumptions is very much harder than is generally believed.
FORMALIZING THE REQUIRED KNOWLEDGE: Just constructing a knowledge base is a major intellectual research problem. Whether one's goal is logistic or not, we still know far too little about the contents and structure of common-sense knowledge. A "minimal" common-sense system must "know" something about cause-and-effect, time, purpose, locality, process, and types of knowledge. It also needs ways to acquire, represent, and use such knowledge. We need a serious epistemological research effort in this area. The essays of McCarthy {} and Sandewall {} are steps in that direction. I have no easy plan for this large enterprise; but the magnitude of the task will certainly depend strongly on the representations chosen, and I think that Logistic is already making trouble.
RELEVANCY: The problem of selecting relevance from excessive variety is a key issue! A modern epistemology will not resemble the old ones! Computational concepts are necessary and novel. Perhaps the better part of knowledge is not "propositional" in character, but inter-propositional. For each "fact" one needs meta-facts about how it is to be used, and when it should not be used. In McCarthy's "Airport" paradigm we see ways to deal with some interactions between "situations, actions, and causal laws" within a restricted microworld of things and actions. But while the system can make deductions implied by its axioms, it cannot be told when it should or should not make such deductions.
For example, one might want to tell the system to "not cross the road if a car is coming." But one cannot demand that the system "prove" no car is coming, for there will not usually be any such proof. In PLANNER, one can direct an attempt to prove that a car IS coming, and if the (limited) deduction attempt ends with "failure," one can act. This cannot be done in a pure logistic system. "Look right, look left" is a first approximation. But if one tells the system the real truth about speeds, blind driveways, probabilities of racing cars whipping around the corner, proof becomes impractical. If it reads in a physics book that intense fields perturb light rays, should it fear that a mad scientist has built an invisible car? We need to represent "usually"! Eventually it must understand the trade-off between mortality and accomplishment, for one can do nothing if paralyzed by fear.
MONOTONICITY: Even if we formulate relevancy restrictions, logistic systems have a problem in using them. In any logistic system, all the axioms are necessarily "permissive"–they all help to permit new inferences to be drawn. Each added axiom means more theorems, none can disappear. There simply is no direct way to add information to tell such the system about kinds of conclusions that should not be drawn! To put it simply: if we adopt enough axioms to deduce what we need, we deduce far too many other things. But if we try to change this by adding axioms about relevancy, we still produce all the unwanted theorems, plus annoying statements about their irrelevancy.
Because Logicians are not concerned with systems that will later be enlarged, they can design axioms that permit only the conclusions they want. In the development of Intelligence the situation is different. One has to learn which features of situations are important, and which kinds of deductions are not to be regarded seriously. The usual reaction to the "liar's paradox" is, after a while, to laugh. The conclusion is not to reject an axiom, but to reject the deduction itself! This raises another issue:
PROCEDURE-CONTROLLING KNOWLEDGE: The separation between axioms and deduction makes it impractical to include classificational knowledge about propositions. Nor can we include knowledge about management of deduction. A paradigm problem is that of axiomatizing everyday concepts of approximation or nearness. One would like nearness to be transitive:
(A near B) AND (B near C) à (A near C)
but unrestricted application of this rule would make everything near everything else. One can try technical tricks like
(A near*1 B) AND (B near*1 C) à (A near*2 C)
and admit only (say) five grades of near*1, near*2, near*3, etc. One might invent analog quantities or parameters. But one cannot (in a Logistic system) decide to make a new kind of "axiom" to prevent applying transitivity after (say) three chained uses, conditionally, unless there is a "good excuse." I do not mean to propose a particular solution to the transitivity of nearness. (To my knowledge, no one has made a creditable proposal about it.) My complaint is that because of acceptance of Logistic, no one has freely explored this kind of procedural restriction.
COMBINATORIAL PROBLEMS: I see no reason to expect these systems to escape combinatorial explosions when given richer knowledge bases. Although we see encouraging demonstrations in microworlds, from time to time, it is common in AI research to encounter high-grade performance on hard puzzles–given just enough information to solve the problem–but this does not often lead to good performance in larger domains.
CONSISTENCY and COMPLETENESS: A human thinker reviews plans and goal-lists as he works, revising his knowledge and policies about using it. One can program some of this into the theorem-proving program itself–but one really wants also to represent it directly, in a natural way, in the declarative corpus–for use in further introspection. Why then do workers try to make logistic systems do the job? A valid reason is that the systems have an attractive simple elegance; if they worked this would be fine. An invalid reason is more often offered: that such systems have a mathematical virtue because they are
(1) Complete–"All true statements can be proven"; and
(2) Consistent–"No false statements can be proven."
It seems not often realized that Completeness is no rare prize. It is a trivial consequence of any exhaustive search procedure, and any system can be "completed" by adjoining to it any other complete system and interlacing the computational steps. Consistency is more refined; it requires one's axioms to imply no contradictions. But I do not believe that consistency is necessary or even desirable in a developing intelligent system. No one is ever completely consistent. What is important is how one handles paradox or conflict, how one learns from mistakes, how one turns aside from suspected inconsistencies.
Because of this kind of misconception, Godel's Incompleteness Theorem has stimulated much foolishness about alleged differences between machines and men. No one seems to have noted its more "logical" interpretation: that enforcing consistency produces limitations. Of course there will be differences between humans (who are demonstrably inconsistent) and machines whose designers have imposed consistency. But it is not inherent in machines that they be programmed only with consistent logical systems. Those "philosophical" discussions all make this quite unnecessary assumption! (I regard the recent demonstration of the consistency of modern set theory, thus, as indicating that set-theory is probably inadequate for our purposes–not as reassuring evidence that set theory is safe to use!)
A famous mathematician, warned that his proof would lead to a paradox if he took one more logical step, replied "Ah, but I shall not take that step." He was completely serious. A large part of ordinary (or even mathematical) knowledge resembles that in dangerous professions: when are certain actions unwise. When are certain approximations safe to use? When do various measures yield sensible estimates? Which self-referent statements are permissible if not carried too far? Concepts like "nearness" are to valuable to give up just because no one can exhibit satisfactory axioms for them. To summarize:
"Logical" reasoning is not flexible enough to serve as a basis for thinking; I prefer to think of it as a collection of heuristic methods, effective only when applied to starkly simplified schematic plans. The Consistency that Logic demands is not otherwise usually available–and probably not even desirable–because consistent systems are likely to be too "weak.
I doubt the feasibility of representing ordinary knowledge effectively in the form of many small, independently "true" propositions.
The strategy of complete separation of specific knowledge from general rules of inference is much too radical. We need more direct ways for linking fragments of knowledge to advice about how they are to be used.
It was long believed that it was crucial to make all knowledge accessible to deduction in the form of declarative statements; but this seems less urgent as we learn ways to manipulate structural and procedural descriptions. I do not mean to suggest that "thinking" can proceed very far without something like "reasoning." We certainly need (and use) something like syllogistic deduction; but I expect mechanisms for doing such things to emerge in any case from processes for "matching" and "instantiation" required for other functions. Traditional formal logic is a technical tool for discussing either everything that can be deduced from some data or whether a certain consequence can be so deduced; it cannot discuss at all what ought to be deduced under ordinary circumstances. Like the abstract theory of Syntax, formal Logic without a powerful procedural semantics cannot deal with meaningful situations.
I cannot state strongly enough my conviction that the preoccupation with Consistency, so valuable for Mathematical Logic, has been incredibly destructive to those working on models of mind. At the popular level it has produced a weird conception of the potential capabilities of machines in general. At the "logical" level it has blocked efforts to represent ordinary knowledge, by presenting an unreachable image of a corpus of context-free "truths" that can stand separately by themselves. This obsession has kept us from seeing that thinking begins with defective networks that are slowly (if ever) refined and updated.
§§§§§
I especially want to acknowledge the influence of S. A. Papert and of my former students Daniel Bobrow, Eugene Charniak, Bertram Raphael, William Martin, Joel Moses, and Patrick Winston, as well as the more specific contributions of Ira Goldstein, Gerald Sussman, Scott Fahlman, Andee Rubin, Stephen Smoliar, Marvin Denicoff, Ben Kuipers, Michael Freiling and others who have commented on early versions of the manuscript.
Bibliography
{Abelson 1973} R. P. Abelson, The structure of Belief Systems, (in Schank and Colby, 1973)
{Bartlett 1967} F. C. Bartlett, Remembering, Cambridge Univ. Press, 1967
{Berlin 1957} I. Berlin, The Hedgehog and the Fox, New American Library, N.Y., 1957
{Celce-Murcia, 1972} M. Celce-Murcia, Paradigms for Sentence Recognition, UCLA Dept. of Linguistics, 1972
{Chafe 1972} W. Chafe, First Tech. Report, Contrastive Semantics Project, Dept. of Linguistics, Berkeley, 1972
{Chomsky 1957} N. Chomsky, Syntactic Structures, Mouton, 1957
{Fillmore 1968} C. J. Fillmore, The Case for Case, In Bach and Harms, Ed.; Universals in Linguistic theory, Chicago, Holt Rinehart and Winston, 1968
{Freeman-Newell 1971} P. Freeman and A. Newell, A Model for Functional Reasoning in Design, Proc. Second Intl. Conf. on Artificial Intelligence, London, Sept. 1971
{Goldstein 1974} I. P. Goldstein, Understanding Fixed-Instruction Turtle Programs, MIT Artificial Intelligence Laboratory Tech. Rept TR-294
{Gombrich 1969} E.H. Gombrich, Art and Illusion, Princeton 1969
{Guzman 1967} A. Guzman, Some Aspects of pattern recognition by Computer, MS Thesis, MIT, Feb. 1967
{Guzman 1969} A. Guzman, Computer Recognition of Three Dimensional Objects in a Visual Scene, Thesis, MIT, Dec. 1969
{Hogarth 1753} W. Hogarth, The Analysis of Beauty, Oxford 1955
{Huffman 1970} Huffman, D. A., Impossible Objects as Nonsense Sentences, Machine Intelligence 6, Edinburgh Univ. Press, 1970
{Koffka 1963} K. Koffka, Principles of Gestalt Psychology, Harcourt, Brace and World, New York, 1963
{Kuhn 1970} T. Kuhn, The Structure of Scientific Revolutions, Univ. of Chicago Press, (2nd Ed.) 1970
{Lavoisier 1783} A. Lavoisier, Elements of Chemistry, Regnery, Chicago, 1949
{Levin 1973} J. A. Levin, Network representation and Rotation of letters, Dept. of Psychology, USCD, La Jolla, Calif 92037, Sept. l973
{Martin 1974} W. Martin, Memos on the OWL System, MIT, l974
{McDermott 1974} D. McDermott, Assimilation of new information by a natural language understanding system, MIT Artificial Intelligence Laboratory Tech. Rept. AI TR-298, March 1974.
{McDermott-Sussman 1972} D. McDermott and G. J. Sussman, The CONNIVER Reference Manual, AI Memo 259, May 1972.
{Minsky 1972} M. Minsky, Form and Content in Computer Science, J.A.C.M., Jan 1972
{Minsky-Papert 1969} M. Minsky and S. Papert, Perceptrons, MIT Press, 1969
{Minsky-Papert 1972} M. Minsky and S. Papert, "Progress Report on Artificial Intelligence," AI Memo 252, MIT Artificial Intelligence Laboratory, Cambridge, Mass., Jan. 1972
{Moore-Newell 1973} J. Moore and A. Newell, How can MERLIN Understand? in Knowledge and Cognition, J. Gregg, Ed., Lawrence Erlbaum Associates, Potomac Md. 1973
{Newell 1973} A. Newell, Production Systems: Models of Control Structures, Visual Information Processing, Academic Press, 1973
{Newell 1973} Allen Newell, Artificial Intelligence and the Concept of Mind, in Schank and Colby, 1973.
{Newell-Simon 1972} A. Newell and H.A. Simon, Human Problem Solving, Prentice-Hall 1972
{Norman 1972} D. Norman, Memory, Knowledge and the answering of questions, Loyola Symposium on Cognitive Psychology, Chicago 1972.
{Papert 1972} S. Papert, Teaching Children to be Mathematicians Versus Teaching About Mathematics, Int. J. Math. Educ. Sci. Technol., vol. 3, 249-262, 1972
{Piaget 1968} J. Piaget, Six Psychological Studies, (D. Elkind, Ed), Vintage, N. Y.,1968
{Piaget-Inhelder 1956} J. Piaget and B. Inhelder, The Child's Conception of Space, The Humanities Press, N.Y.,1956
{H. Poincare, 1913} The Foundations of Science, trans. G.B. Halstead, 1913}
{Pylyshyn 1973} Z.W.Pylyshyn, What the Mind's Eye tells the Mind's Brain, Psychological Bulletin, vol. 80, pp1-24, 1973
{Roberts 1965} L. G. Roberts, "Machine Perception of Three Dimensional Solids", Optical and Optoelectric Information Processing, MIT Press, 1965
{Sandewall 1970} E. Sandewall, Representing Natural Language Information in Predicate Calculus, in Machine Intelligence, Vol. 6, Edinburgh, 1970
{Schank 1972} R. Schank, "Conceptual Dependency: A Theory of Natural Language Understanding," Cognitive Psychology, pp552-631, 1972
{Schank-Colby 1973} R. Schank and K. Colby, Computer Models of Thought and Language, Freeman, San Francisco, 1973
{Simmons 1973} R. F. Simmons, Semantic networks: Their Computation and use for Understanding English Sentences, in Schank and Colby, 1973
{Sussman 1973} G. J. Sussman, A Computational Model of Skill Acquisition, MIT Artificial Intelligence Laboratory Tech. Rept AI TR-297 1973
{Underwood-Gates 1972} S.A. Underwood and C.L.Gates, Visual Learning and Recognition by Computer, TR-123, Elect. Res. Center, University of Texas, April 1972
{von Neumann 1955, Mathematical Foundations of Quantum Mechanics, Princeton Univ. Press, 1955
{Waltz 1972} D. L. Waltz, Generating Semantic Descriptions from Drawings of scenes with Shadows, MIT Thesis, Nov. 1972
{Wertheimer 1959} M. Wertheimer, Productive Thinking, Harper and Row, 1959
{Wilks 1973} Y. Wilks, Preference Semantics, Stanford Artificial Intelligence Laboratory Memo AIM-206, Stanford University, July 1973
{Wilks 1973} Y. Wilks, An Artificial Intelligence Approach to Machine Translation, in} Schank and Colby, 1973
===