Henry Lieberman
and University of Paris 6 Pierre and Marie Curie
4, place Jussieu
75252 Paris Cedex 05 France
In many situations involving highly connected networks of objects, such as semantic networks in AI, hypermedia networks, or scene representations in computer graphics, the notion of "current viewpoint" or "current focus of attention" is important. In traditional systems, the network structures are considered relatively fixed, while the user's viewpoint is considered to move through the structure. But it is also possible to take the alternative approach, where the viewpoint is considered fixed and the surrounding structure is constantly changing to maintain the consistency of the user's viewpoint. As the theory of relativity asserts the equivalence of all frames of reference, this unconventional approach is just as good as the traditional one. But keeping a fixed viewpoint has significant advantages for algorithms in which the current viewpoint plays an important role.
I present a system that uses a process of "re-rooting" called marcottage, to implement this approach. Whenever a link is followed in this system, the system conceptually reverses the link. This leads to a kind of navigational programming style which has some distinct advantages [as well as disadvantages] compared to the traditional one. The entire network remains accessible from any particular viewpoint, and it is easy to implement reversible algorithms or "undo" operations. An incremental change operation is provided which appears to the user as if the entire network has been modified, but in fact all state is preserved, and information is copied only as needed to maintain this illusion. This incremental change operation is useful, for example, in making private annotations to hypermedia networks, counterfactuals in knowledge bases, or incremental redisplay algorithms in computer graphics.
Marcotte: A part of a plant capable of regenerating missing parts, thus propagating a new plant capable of independent growth.
from the French Botanical Dictionary
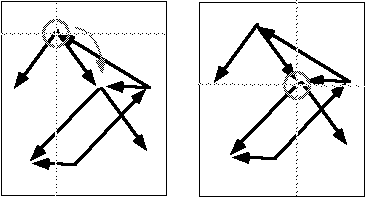
Two possibilities for the representation of movement:
Move the focus or move the context?
Suppose you are driving a car through the streets of a city. Consider two different representations of the movement of the car through the city. The first representation is a map of the city, a static network of connections between streets. The itinerary of the car could be represented by a moving point indicating the instantaneous position of the car at every moment. The other representation is what the driver sees through the windshield. From his or her point of view, it is the position of the car that is fixed, and it is the visible pattern of streets that changes at each instant.

Two possibilities for the representation of movement. Above, a static network with the focus point circled. The network stays the same in both pictures, and the focus point moves.
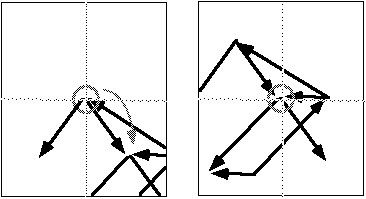
Here, the focus point remains the same in both views, and it is the network that moves.
The two points of view are, in a certain sense, equivalent. The theory of relativity asserts the equivalence of any physical frame of reference. But the two points of view are not, however, identical. For some purposes, one or the other is superior. For planning an itinerary through a city, the global perspective of a street map is preferable. But the driver of a car seeking a destination has a "navigational" task to perform, and justifiably prefers the view though the windshield, which gives priority to the local position.
Traditional object-oriented programming gives priority to the first approach. A network of objects connected by instance and inheritance links is considered relatively static, and a program that operates by sending messages, and accessing methods and instance variables is conceptually considered to "move" through this structure. In this paper, I explore the inverse approach. I show how to implement objects that "move" the surrounding context whenever a shift in position is made, to give the appearance of a "fixed" viewpoint.
The French word marcottage is a botanical term for the propagation of plants like strawberries that are capable of sending out a branch or shoot, which, landing on the ground, establishes a new set of roots. If the plant is considered to be "located" at its root, marcottage presents a philosophical problem: where is the plant really located now? It is possible to shift the point of view so that the plant is considered to be located at its new root, and the old root is considered to be a "branch". I introduce objects called marcottes which perform an analogous function in object networks. It is these objects that perform the context shift that moves objects around a fixed viewpoint.
Two systems of marcottage: Binary trees and CLOS objects
I present two versions of systems using the marcottage technique. The first uses an object-oriented representation of binary trees. This one will be the simplest to explain, and the correspondence with Lisp and with classical object-oriented techniques will be the most evident. I will use this system to illustrate how marcottage facilitates implementing reversible tree walk algorithms and supports an unusual incremental modification operation.
The second system is more general, and implements marcottage operations for arbitrary CLOS objects [Keene 1988] and their instance variables. It is this second system that truly supports a navigational programming style. I will discuss the pros and cons of this style. Finally, I will discuss applications areas which can benefit from the marcottage technique.
Marcottage of binary trees
Let's start with an object-oriented representation of binary trees. This consists of an abstract class NODE, and two sub-classes: LEAF, which represents a terminal node, and TREE, which has two instance variables representing subtrees: LEFT-SIDE and RIGHT-SIDE. CLOS code is presented in the appendix.
Direct access to the subtrees through the instance variables LEFT-SIDE and RIGHT-SIDE is strongly discouraged when using the marcottage technique. Instead, the abstract functions LEFT and RIGHT are provided. LEFT and RIGHT differ from LEFT-SIDE and RIGHT-SIDE in that they create marcotte objects that represent each of the subtrees. A marcotte object also stores the access path by which the object is reached.
Conceptually, each time you follow a link between a tree and a subtree, the direction of the link is "inverted". The result can be considered as a new tree that has the subtree as its root. The tree is thus "re-rooted". This is illustrated below.
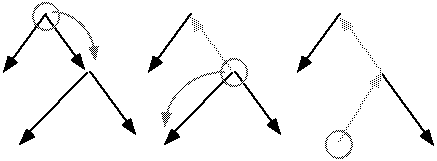
The marcottage operation can be viewed as a reversal of the direction of links. The circle denotes the root of the tree. The middle part of the illustration represents the result of following the link leading to the right of the top root. Reversed links are shown in gray. At right is the result of following a link to the left.
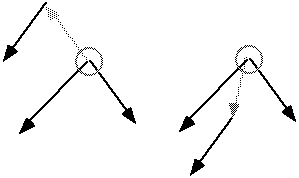
Another view of the marcottage operation is as a "re-rooting" of the tree. Passing from one node to another amounts to replacing the tree with another that has the destination node as its root and the same connectivity as the original. At left, the second part of the preceding illustration. At right, a tree having a the circled node as its root, and the same connectivity.
For each marcotte, the function UP follows the reversed link. Because of this, every marcotte "knows where it came from". Unlike traditional tree walk procedures, walking a structure by marcottage preserves all information in the structure. The entire structure remains accessible from any location within it.
Link reversal can be implemented non-destructively
If the operations LEFT and RIGHT were implemented by physically reversing the pointers, they would be destructive. It is preferable to have operations that preserve the state of the original structure. The marcottage operations can be implemented in a way that creates new objects instead of destructively modifying the contents of instance variables.
A marcotte is an object composed of three elements: the "new root", the "original root", and the access path, called respectively DOWN, UP and DIRECTION. The functions LEFT and RIGHT create an object which has as destination DOWN, the original tree as UP, and a symbol LEFT or RIGHT for DIRECTION.
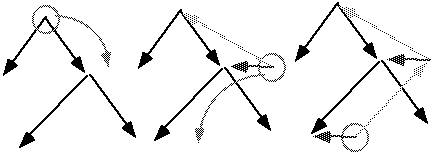
Pointer "reversal" is actually accomplished by creating new objects. To follow the subtree to the right of the root, a new object is created which has the destination subtree as DOWN and the original tree as UP. At right, the tree walk to the left creates an object for which UP is the marcotte created during the previous step.
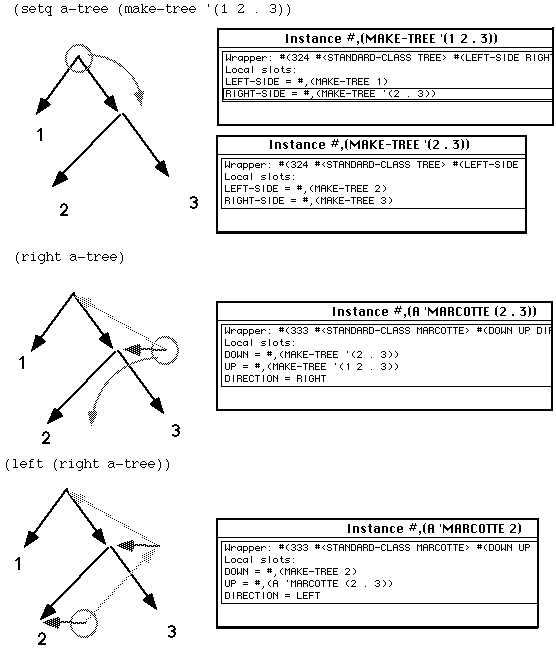
The next illustration shows the structure of marcotte objects as they appear textually in the Lisp browser. A function MAKE-TREE establishes the correspondence between Lisp S-expressions and CLOS objects. The printer is extended to print NODE, TREE and MARCOTTE objects as their associated S-expressions preceded by the character "#" which permits the Lisp reader to reconstruct a similar object.
An application of marcotte objects: A reversible, incremental tree walk
Many algorithms are based on recursive tree walk or other network traversal procedures. Marcottes provide a means of easily implementing such traversals in a lazy or incremental fashion. Each marcotte object knows its position in the traversal process, and can calculate the "next position" or "previous position" when necessary.
Since marcottage preserves the connectivity of the structure, it is also easily possible to reverse the direction of any traversal. The inverted traversal follows a procedure symmetric to the forward traversal. The direction can even be changed in mid-course or changed repeatedly. Using Lisp lists or conventional doubly-linked lists would require a more complicated management of pointers.
The appendix presents code for both forward and backward traversal algorithms. A forward traversal consists of a classical lazy recursive depth-first tree-walk, using the accessor operations LEFT and RIGHT. The traversal proceeds to the left until it finds a terminal node, then ascends to the next higher level and continues to the right. Traversal in the reverse direction proceeds symmetrically, following the left subtree whenever the right subtree is exhausted.
It is also possible to define other traversal strategies, such as breadth-first search. [Krief 90] presents a system which is capable of generating user interface code from a definition of a traversal strategy. This suggests an approach to the automatic creating of browsing interfaces from the definition of marcottage traversals.
The next illustration shows a sequence of tree traversal steps, in both the graphic and S-expression representations.

The reversible tree-walk algorithm is a good illustration of the navigational aspect of marcottage programming. Each step is treated strictly from a localized point of view, with all the momentary state of the process recorded in the marcotte objects. What classical algorithms store on the recursive call stack is here represented by the UP links and reversibility is obtained by the traversal of such links. Marcottage gains power from removing the reliance on stacks, continuations, or other structures external to the objects being traversed.
Marcottes can be edited without destructive modification
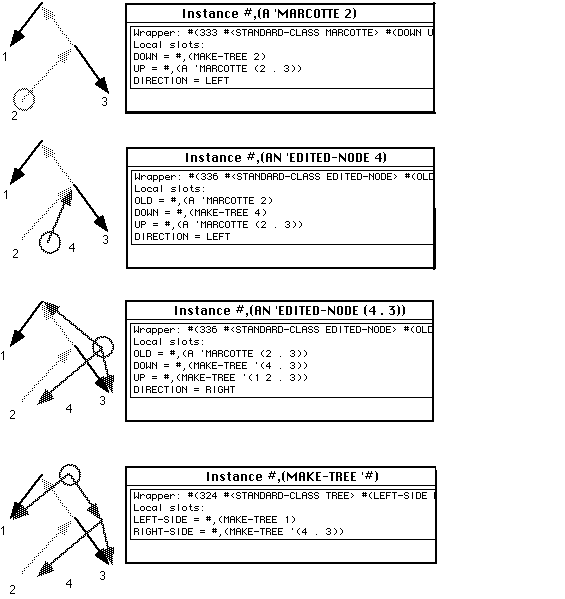
We have illustrated above how reversibility can be implemented without destructive modification. What is even more surprising, perhaps, is that these structures can even be edited without destructive modification! We introduce a novel replacement operation which has the effect of creating a "virtual copy" of the entire network, with the new component replacing the old, and preserving the same connectivity for all the other components. Marcottage assures that only the portion of the structure that has changed is copied, in a lazy and incremental manner. The function REPLACE-MARCOTTE accepts as argument a marcotte, together with a new object to serve as replacement. This operation returns an object of class EDITED-NODE which represents the modified structure.
The next page shows the replacement process. In the first part, the marcotte representing the node 2 is shown, following the path first to the right, then to the left of the root. The second part shows the result of a call to REPLACE-MARCOTTE to substitute a node labeled 4 for the node 2. The resulting object is an EDITED-NODE, which inherits the attributes of a marcotte: the instance variables UP, DOWN, and DIRECTION. UP and DIRECTION are copied from the original marcotte. The variables UP and DIRECTION assure that the EDITED-NODE possesses the same position in the hierarchy occupied by the original node. DOWN is the new object, the node 4 in the example. The original node 2 is saved as the value of the variable OLD. The EDITED-NODE retains the replaced object to perform the incremental substitution of changed structures during the process of going back through the UP link. Because of this, it is also possible to implement a REVERT operation which reconstructs the original structure before the edit.
The last two parts of the illustration show the results of two successive UP operations. The first result is also an EDITED-NODE. To construct the new DOWN part, the old UP link is followed, leading to the tree (2 . 3). The LEFT direction indicator directs the replacement of the subtree 2 with the new element 4, so that the result is a new tree (4 . 3). The final part of the illustration shows the result of applying this operation one more time, finally arriving at the top of the tree. The result is identical to what would have resulted from the call (MAKE-TREE '(1 4 . 3)), except that the subtrees 1 and 3 are shared with the original structure.
Notice that the original tree (MAKE-TREE '(1 2 . 3)) rests unchanged by this operation. From the point of view of a program which uses the EDITED-NODE labeled 4 in place of the marcotte labeled 2, it is exactly the same as if the structure had been edited. Notice also that it is possible to begin traversing the structure, make some edits, and continue the traversal, forward or backward, in a transparent manner.
A CLOS object can access its instance variables through marcottage
Now, we extend the approach used above for binary trees to show how the marcottage technique can apply to more general objects, CLOS instances. A CLOS instance is composed of classes and instance variables. The value of each one of those instance variables is in turn a CLOS object, so that all the objects in a system at a given time form a connected network. The technique of object-oriented programming often consists of traversal of this network by chains of references to instance variables, modifications of values of instance variables, and creation of new objects. It is in the traversal and modification phases that the marcottage technique can have impact.
The new approach to object-oriented programming that I am proposing here consists of using marcottage for the reference and modification of instance variables. In traditional object-oriented languages, an instance is linked to its instance variable by a unidirectional link. The message or access function returns the value of the variable. It loses the reference to the original object, if that object is not saved independently as the value of another variable [or perhaps referenced by the pseudo-variable SELF]. The creation of new objects is relatively rare compared to variable access. In the classical object-oriented technique, the network is thus considered relatively static, while a user program that follows instance variable or class links "jumps" from one object to another, changing its point of view at each step.
On the other hand, if an object references its instance variables by marcottage, each reference creates a marcotte designating the value of the variable. Conceptually, each marcotte inverts the link to point from the value of the instance variable to its containing instance. In this way, the entire network remains accessible from any location within it. The UP message is accepted by all marcottes, permitting the chain of references to be traversed in the opposite direction at any moment. Thus, the point of view of a user program stays relatively fixed, while the relations between objects change to reflect the movement of viewpoint.
Next, I present an example of marcottage of a system of objects. Let's imagine that we have graphical objects representing the parts of a house: the wall, door, windows, roof. They are arranged in a part-whole hierarchy, as is common in scene representations in computer graphics. When a whole references a part [such as a reference from the HOUSE to the WALL], we create a marcotte object. The function UP applied to the marcotte for the WALL results in the original HOUSE. It is quite possible to have two different marcottes to the same WALL, for example if two neighboring houses shared the same wall. In such a case, the wall is identical, but the marcottes can be distinguished by the value produced by UP.
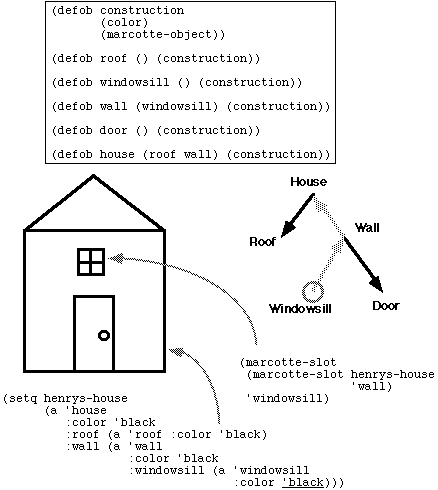
The editing of graphical objects illustrates some of the advantages of the marcottage approach. If the user would like to edit an object described by a chain of references, for example, the COLOR of the WINDOWSILL of the WALL of the HOUSE, the function REPLACE-MARCOTTE can perform the edit directly, without the need to explicitly modify all the containing structures. The result of a call to REPLACE-MARCOTTE is the new COLOR, but the path that lead to the edit is retained implicitly by the marcotte objects. Subsequent iterated calls to UP to climb the structure has the effect of incrementally reconstructing the new house having the recolored windowsill.

This approach should be useful in computer graphics to implement the important task of incremental redisplay. Because the edit does not destroy the original object, a sequence of replacement operations to widespread parts of the structure can be performed, and the result compared with an unmodified version saved during the last redisplay period. The substructures which have changed since the last redisplay and require redisplay during the next pass simply "fall out" of a recursive comparison. Marcottage provides a technique for implementing an application-independent incremental redisplay. This generalizes the incremental redisplay strategy used in many interactive systems, notably Emacs [Stallman 84].
The implementation of marcottage in CLOS
Our current implementation of marcottage in CLOS defines an object MARCOTTE-OBJECT which gives objects that inherit from it the behavior of marcottage of instance variables. The implementation resembles that previously described for binary trees, although the notion of DIRECTION is replaced by the SLOT-NAME of the CLOS object. To access the object denoted by a marcotte, it is necessary to explicitly dereference the marcotte by the function DOWN. Details of the implementation are presented in the appendix.
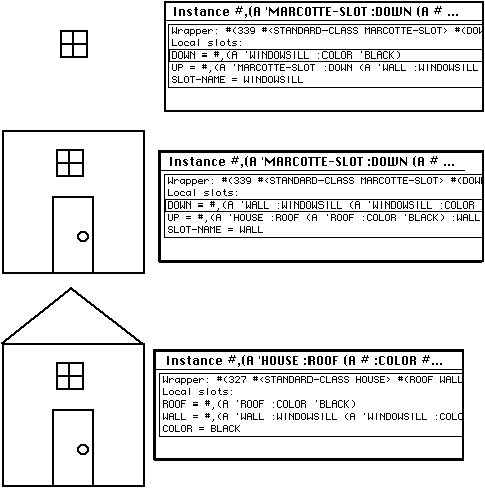
Objects corresponding to a marcotte (windowsill (wall (a 'house)))
For the moment, we choose not to disturb the normal behavior of the standard CLOS instance variable access and modification operations. Instead, new functions are added that perform the marcottage versions of these operations. We define a function MARCOTTE-SLOT which is the equivalent of SLOT-VALUE of CLOS. The usual behavior of SLOT-VALUE remains accessible. Similarly, the function REPLACE-MARCOTTE is the equivalent of SETF for the SLOT-VALUE.
However, this approach is not completely satisfactory. The user is burdened with having to mention explicitly the treatment of objects as marcottes. In a system that universally applied the marcottage technique, SLOT-VALUE would have the behavior of MARCOTTE-SLOT and SETF would be the same as REPLACE-MARCOTTE. The need to explicitly call the function DOWN would be largely eliminated. In order to accomplish this transparently, the ability to forward non-marcotte messages from a marcotte to the object it denotes by DOWN is essential. This requires a delegation mechanism [Lieberman 86], [Stein, Lieberman, Ungar 89], [Ungar and Smith 87]. The question remains open whether or not the meta-object protocol of CLOS [Cointe, Graube 88] is sufficient to accomplish this radical language extension. This might make a good test of the extensibility claimed for CLOS by its authors. Pierre Cointe of the University of Paris 6 and Rank Xerox France is currently exploring an implementation using meta-classes in Smalltalk-80.
The analogy between marcottage of trees and marcottage of CLOS objects suggests that the traversal operations FORWARD and BACKWARD also make sense for general CLOS objects. It is quite unusual in object-oriented systems to take advantage of the order of definition of instance variables to order the traversal, but this natural ordering is useful in defining a traversal independent of the names attached to slots. In the absence of a canonical default ordering, the traversal must be defined anew for each kind of object traversed. The convenience of defining general traversal algorithms can often outweigh the loss of encapsulation implied by reliance on implementation-dependent ordering.
Marcottage: A new programming paradigm for objects
Marcottage introduces its own unique programming style, which requires both a period of familiarization, and a fundamentally different attitude with regard to the use of objects in programming. The biggest difference is adopting the "navigational" viewpoint, which emphasizes locality of reference in object networks.
A principal use of variables in object-oriented languages is as bookmarks. A bookmark is used to serve as a placeholder to remember a specific location deemed significant. Later reference to the bookmark can be used to retrieve that location regardless of what intervening activities have taken place. When a message is sent to the value of an instance variable, if the target of the message needs to know the location referenced by the bookmark, the bookmark variable is passed as an argument.
Programming with marcottage has the effect of significantly reducing the need for such bookmarks. There is no need to explicitly save a location if it can always be accessed by inverting the path which led to it. The path itself implicitly serves the same function as the bookmark. The result is a simplification of algorithms for which the reference structure is primarily localized [and, of course, a corresponding increase in complexity for algorithms whose reference structure often "jumps" from place to place]. When editing structures with REPLACE-MARCOTTE, jumps should be avoided, but the retraversal of paths implicitly performs an incremental update which might otherwise be more complicated.
One consequence of the object creation that occurs during traversal of marcotte paths is that more care must be taken with the EQ comparison of object identity. Due to the fact that two marcottes to the same object are not EQ, the function DOWN must dereference the marcottes before comparison. Alternatively, a new equality predicate that automatically dereferences marcottes could be defined. Another consequence has to do with memory allocation. "Inverted" pointers may prevent the garbage collector from recovering structures that are not otherwise referenced.
Marcottage of generalized structures
Until now, we have only discussed the case where marcotte objects do not share substructure. Certainly, this is always the case with binary trees. Shared subtrees, as generated by shared values of instance variables of CLOS objects, do not pose any problem for traversal, because they are always distinguished by the uniqueness of their access paths. For replacement of shared or circular structures, there is a question of what the correct semantics is for this operation.
The situation is in some ways analogous to that of multiple inheritance in object-oriented languages, for which the debate still rages in the programming language community. [Briot 75] is a good analysis of the problems and possibilities concerning multiple inheritance.
The obvious extension to deal with the problem of shared substructures requires a change to the function UP to deal with edited marcottes. The version presented in the appendix uses the function REPLACE-MARCOTTE to make the substitution of the edited object in the containing structure. This substitution only happens during the traversal of pointers inverted by marcottage. But in the case of shared substructures, it is also possible to arrive at the edit point by other paths. It is then necessary to guarantee that the function UP, in the same manner as EDITED-MARCOTTE, always produces objects capable of applying the same substitution during subsequent marcottage.
Is marcottage more expensive than conventional programming?
At first glance, it might appear that the marcottage programming style might prove significantly more expensive than conventional programming. This might seem so because of the number of "extra" objects created during marcottage of instance variables. But this does not necessarily mean that marcottage is more expensive!
It is indeed true that marcottage creates a new object on every access, unlike the traditional instance variable access operation. However, this is not quite so bad as it may seem. First, the rate of object creation is bounded. Each step can create no more than one object. There are "lazy" compilation techniques that can optimize allocation of objects created with such a regular pattern. Second, it is important to note that, if access is the only goal of the traversal, the lifetimes of the objects created are very short.
It is this last point that is significant. With the proper sort of garbage collection algorithm, a steady stream of newly created objects with short lifetimes does not pose a significant storage allocation burden. Using garbage collection algorithms that adapt the rate of garbage collection according to the lifetime of the objects, such as the generational garbage collection algorithm first described in [Lieberman, Hewitt 83], objects with short lifetimes are recovered quickly. These algorithms operate in real time, without requiring any significant pause in computation.
Application of marcottage to a reversible, editable debugger
The application which originally motivated this work on marcottage had to do with an interactive graphical debugger. [Lieberman 84] and [Lieberman 87] describe debuggers which display evaluation as a process of visual substitution. Expressions in the code being evaluated are first highlighted, then replaced by their values. The control structure of these debuggers is reversible, supporting a heuristic debugging strategy which runs a program forward until the occurrence of an error, then backwards to discover the causes of the error.
Marcottage developed as a way of naturally representing a reversible substituting evaluation. A program can be thought of as a tree, evaluation as a traversal process. The reversibility of marcottage traversal leads to a natural evaluation history keeping mechanism. The challenge is then how to edit a program that is in the middle of running. The REPLACE-MARCOTTE operation allows editing the momentary state of a program to correct an error, and to resume running the program, in either direction.
In [Lieberman 89], a kind of visual marcottage is used as a presentation technique in a three-dimensional program visualizer. The function-argument relation in code is represented visually by containment of 3D polyhedra representing expressions. As control passes from one expression to another, the display is "re-rooted" so that the expression of current interest is always the outermost polyhedron. The rest of the display is adjusted at each step to maintain this fixed point of view. A 2D visual marcottage for a knowledge base browser is described in [Travers 89].
An interpreter based on marcottage should also be useful for programming by example [Lieberman 86]. The task of a classical interpreter is to dynamically produce a sequence of evaluation states from a set of function definitions and an expression with concrete values. The function definitions are relatively static and abstract. The goal of programming by example is the inverse. Starting with the steps of the computation in a concrete example, the goal is to synthesize the abstract function definitions. A programming by example system has generalization operation that replace concrete values by their generalizations in terms of variables and function calls. This replacement is a kind of editing that can be readily accomplished with the marcottage technique.
Other application domains: Hypermedia and hypothetical reasoning
The marcottage operations will find utility in many situations requiring editing of interconnected structures, where it is advantageous to avoid destructive modification and global recopying.
One such domain of much current interest is hypertext [or, more generally, hypermedia, which includes graphics, sound, and other media]. Hypermedia is defined as information presented non-sequentially, including dynamic and interactive control of the presentation. A hypermedia system typically consists of a set of screens, each containing text and graphic elements. Each screen contains links, active regions which are sensitive to mouse clicks. When the user clicks on one of the links, another screen [with, in turn, its own graphics, text, and links] is made visible. For example, if the user clicks on a bibliographic reference in a literary work, he or she could be instantly transported to the original source. Obviously, a hypermedia system forms a network of screen objects connected by their interactive links.
A frequently desired capability in such systems is for the user to have the ability to make personal annotations. Perhaps the user would like to add to the system new references unknown to the original author, or add his or her own personal commentary. In conventional hypermedia systems, the user must modify the link structure, in a destructive fashion. But the hypermedia network might be shared by other users who might not be interested in the personal annotations of another user. Even the user who made the modifications in the first place might wish to retain an unmodified copy or undo the annotations. The classical solution would be to create an entire copy of the network, but this would be very slow and space-consuming in a large network.
With marcottage, a marcotte is created upon each traversal of a hypermedia link, and personal annotations can be accomplished with REPLACE-MARCOTTE. The original version remains unchanged. A typical user might only be interested in a small part of a very large network, and cannot follow all the available links. Marcottage assures that only the portion actually traversed by the user will be copied as the result of an annotation. Each annotation only requires a brief computation, preserving the interactivity of the interface.
In artificial intelligence, truth maintenance systems [deKleer 86] are a popular technique for managing assertions in a knowledge base. A truth maintenance system consists of nodes representing facts or hypotheses, connected by links representing the relation of inferential support among them. During the reasoning process, each assertion is labeled with its set of supporting assertions. An assertion can be added or removed, and the system incrementally computes the consequences of that modification. These systems, especially the kind called assumption-based truth maintenance systems, are useful to model hypothetical reasoning.
Typically, it is difficult to decide whether or not it is desirable to add a hypothesis until the consequences of the modification become apparent. This makes reversibility and the ability to undo modifications crucial. Using marcottage to represent the support links between propositions permits the system to cancel undesirable modifications in an efficient and transparent manner. The incremental copying of modified structures also promotes efficiency when hypothetical modifications to a knowledge base are performed frequently.
History and previous work
The idea of navigational representations is not completely new in the history of object-oriented programming. I first encountered this idea in [Baker 78], where a navigational representation [albeit destructive] was used to represent variable bindings. Baker was looking for an efficient means of representing changes in the variable environment, which can be construed as the instantaneous "point of view" of the evaluation of a Lisp program. The Deutsch-Schorr-Waite garbage collection algorithm [Cohen 87] used a "pointer inversion" technique [again, destructive] to avoid management of the stack during the traversal of accessible pointers. Other specialized uses of analogous techniques can be found in the literature, especially in the literature of functional programming and logic programming. The techniques for using "virtual copies" to simulate destructive modification are similar to those found in [Mittal, Bobrow and Kahn 86].
More recently, I was inspired by the work of Michael Travers [Travers 89], who implemented a graphical browser called MUE for the CYC knowledge base. The goal of this browser is to help the user navigate through a knowledge base much too large to be comprehended in any sort of global view. Containment of icons is used as a kind of visual marcottage for presenting descriptions in the knowledge base. I used a similar principle in a 3D program visualization system [Lieberman 89].
The major contribution of the present work consists in the realization that marcottage is a general technique for implementing navigational algorithms, and can be implemented in an application-independent manner. I have shown how marcottage can also be implemented with non-destructive operations, and how reversible traversal algorithms and incremental modification can be defined. Finally, marcottage can be used as the basis of a fundamentally different relation between an object and its instance variables.
Appendix: The CLOS code for marcottage
This code is written in Apple Macintosh Allegro [Coral] Common Lisp 2.0, using CLOS, the Common Lisp Object System [Keene 88]. Only the most important details are presented because of space considerations.
We start with the code for marcottage of binary trees. First, we show the object-oriented representation of the trees, coded with some minor syntactic extensions to CLOS. The macro DEFOB is a simplified version of CLOS's DEFCLASS. The list of instance variables and their initializations precedes the list of classes from which the defined class inherits. DEFOB constructs the functions for variable access automatically. The macros A and AN are synonyms of MAKE-INSTANCE, simply to improve conciseness and readability.
(defob node ())Now, here is the representation of marcottes. The abstract accessor functions LEFT and RIGHT create marcottes which are linked to their originating objects.
(defob null-node () (node))
(defob leaf ((name nil)) (node))
(defob tree
((left-side (a 'null-node))
(right-side (a 'null-node)))
(node))
MAKE-TREE converts Lisp expressions into the object-oriented tree representation.
(defun make-tree (sexp)
(cond ((null sexp) (a 'null-node))
((typep sexp 'node) sexp)
((atom sexp) (a 'leaf :name sexp))
((a 'tree
:left-side (make-tree (car sexp))
:right-side (make-tree (cdr sexp))))))
Functions which operate on trees are also extended to operate on marcottes through a call to DOWN, as illustrated in the following example.(defob marcotte ((down nil) (up nil) (direction nil)) (node))
(defmethod left ((self tree))
(a 'marcotte :up self :down (left-side self) :direction 'left))
(defmethod right ((self tree))
(a 'marcotte :up self :down (right-side self) :direction 'right))
(defmethod left ((self marcotte))(a 'marcotte :up self :down (left-side (down self)) :direction 'left))
Here is the code for a traversal of a tree in the forward direction. The function descends recursively to the left until it reaches a leaf node. The function FORWARD-UP does the equivalent of a "return", climbing up the hierarchy. If the search had descended to the left, it continues to the right. If the search had been to the right, it then ascends to the next level.
The function BACKWARD does a traversal in the reverse direction, by a process symmetric to that performed by FORWARD.(defmethod forward ((self null-node)) nil)
(defmethod forward ((self leaf)) nil)
(defmethod forward ((self tree)) (left self))
(defmethod forward ((self marcotte))
(cond ((leaf? self) (forward-up self (up self)))
((left self))))
(defmethod forward-up ((self marcotte) higher)
(cond ((eq (direction self) 'left) (right higher))
((eq (direction self) 'right)
(forward-up higher (up higher)))
((error "FORWARD-UP: ~S is neither right nor left of ~S"
self higher))))
(defmethod forward-up ((self marcotte) (higher null)) nil)
(defmethod forward-up ((self tree) (higher null)) nil)
The following code shows how marcottes are edited. An editing operation creates an object of class EDITED-NODE which stores both the object before editing, and its replacement.(defmethod backward ((self null-node)) nil)
(defmethod backward ((self leaf)) nil)
(defmethod backward ((self tree)) nil)
(defmethod backward ((self marcotte))
(backward-up self (up self)))
(defmethod backward-up ((self marcotte) higher)
(cond ((eq (direction self) 'right)
(backward-down (left higher)))
((eq (direction self) 'left) higher)
((error "backward-UP: ~S is neither left nor right of ~S"
self higher))))
(defmethod backward-down ((self marcotte))
(cond ((leaf? self) self)
((backward-down (right self)))))
(defmethod backward-up ((self marcotte) (higher null)) self)
(defmethod backward-up ((self tree) (higher null)) self)
(defob edited-node ((old nil)) (marcotte))The semantics of UP applied to an EDITED-NODE differs from that of an ordinary MARCOTTE. The substructures which has been edited is replaced according to the direction of the marcotte.
(defmethod replace-marcotte ((self null-node) new) nil)
(defmethod replace-marcotte ((self t) new) new)
(defmethod replace-marcotte ((self marcotte) new)
(an 'edited-node
:down new
:old self
:up (up self)
:direction (direction self)))
Marcottage of CLOS objects(defmethod up ((self edited-node))
(replace-marcotte
(slot-value self 'up)
(replace-inferior (down (slot-value self 'up))
(direction self)
(down self))))
(defmethod replace-inferior ((self tree) direction new)
(cond ((eq direction 'left) (create self :left-side new))
((eq direction 'right) (create self :right-side new))
(self)))
Here, we present the marcottage technique applied to general CLOS objects. MARCOTTE-OBJECT is a "mixin" which should appear in the list of superclasses of any class which would like to make use of marcottage to access its instance variables.
Each instance variable access creates a MARCOTTE-SLOT object. This is the marcottage version of CLOS's SLOT-VALUE function.(defob marcotte-object ())
This is the representation of a marcotte associated with an instance variable or slot.
(defob marcotte-slot
((down nil) (up nil) (slot-name nil))
(marcotte-object))
Functions which operate on MARCOTTE-OBJECT are generalized to apply to MARCOTTE-SLOT objects, via DOWN.
(defmethod marcotte-slot ((self marcotte-object) slot-name)
(a 'marcotte-slot
:down (slot-value self slot-name)
:up self
:slot-name slot-name))
(defmethod marcotte-slot ((self marcotte-slot) slot-name)Unlike the case of trees, the definition of methods associated with a MARCOTTE-OBJECT might require the introduction of new methods on MARCOTTE-SLOT. Delegation of messages would be the best solution here.(a 'marcotte-slot
:down (slot-value (down self) slot-name)
:up self
:slot-name slot-name))
Here are the methods for editing marcottes of CLOS instance variables. Editing creates an EDITED-MARCOTTE object. But the substitution mandated by the edit is not performed immediately.
The substitution is actually performed by the UP function. This delays the actual construction of an edited object until it is absolutely necessary. The function CREATE makes a "differential copy" of its first argument. The other arguments provide the new values of slots which differ from the original. KEYWORD-INTERN produces the keyword, prefixed by a colon, associated with SLOT-NAME.(defob edited-marcotte ((old nil)) (marcotte-slot))
(defmethod replace-marcotte ((self marcotte-object) new) new)
(defmethod replace-marcotte ((self marcotte-slot) new)
(an 'edited-marcotte
:old self
:down new
:up (up self)
:slot-name (slot-name self)))
(defmethod up ((self edited-marcotte))
(replace-marcotte (slot-value self 'up)
(replace-slot (down (slot-value self 'up))
(slot-name self)
(down self))))
(defmethod replace-slot ((self marcotte-object) slot-name new)
(create self (keyword-intern slot-name) new))
Acknowledgments
I would like to thank the group LITP/RXF of the University of Paris 6 and Rank Xerox France for their hospitality and friendship during my year in Paris. Pierre Cointe, Jean-Pierre Briot, Sylvie Lemarié, Christophe Dony and Philippe Gautron provided helpful comments and ideas.
This research has been sponsored by a grant from Hewlett-Packard. I would like to thank Mike Foreman and Pankaj Garg at HP, and Muriel Cooper and Nicholas Negroponte at the MIT Media Lab for their support during my stay in France.
Bibliography
Baker 1978
Henry Baker, Shallow Binding in Lisp 1.5. Communications of the ACM, Vol. 21, No. 7, July 1978.
Briot 1985
Jean-Pierre Briot, Instanciation et héritage dans les langages objets. Thèse de 3ème cycle, Université de Paris VI, LITP Rapport de Recherche 85-21, mai 1985.
Cohen 1987
Jacques Cohen, A Survey of Algorithms for Automatic Storage Management. ACM Computing Surveys, 1987.
Cointe, Graube 1988
Programming with Metaclasses in CLOS. Proceedings of the First CLOS Users and Implementors Workshop, Xerox Parc, Palo Alto, California, USA, October 1988.
deKleer 1986
Johan deKleer, An Assumption-Based Truth Maintenance System. Artificial Intelligence Journal 28 (163-196), 1986.
Keene 1988
Sonya Keene, A Programmer's Introduction to CLOS. Symbolics Press, 1988.
Krief 1990
M.PV.C : Une méthode générale pour l'implémentation de systèmes actifs de spécification, d'interprétation, et de simulation dans un environnement objet. Deuxièmes Journées Internationales de Génie Logiciel et ses Applications. Toulouse, 1989.
Lieberman, Hewitt 1983
Henry Lieberman and Carl Hewitt, A Real-Time Garbage Collector Based on the Lifetimes of Objects. Communications of the ACM, June 1983.
Lieberman 1984
Henry Lieberman, Steps Toward Better Debugging Tools for Lisp, Proceedings of the Third ACM Conference on Lisp and Functional Programming, Austin, Texas, USA, August 1984.
Lieberman 1985
Henry Lieberman, Delegation and Inheritance: Two mechanisms for sharing knowledge in object-oriented systems. 3ème Journées d'études langages orientés objets, Bigre + Globule, Paris, janvier 1985.
Lieberman 1986
Henry Lieberman, An Example-Oriented Environment for Beginning Programmers, in Lawler and Yazdani, eds., Artificial Intelligence and Education, John Wiley and Sons, Chichester, UK, 1986.
Lieberman 1987
Henry Lieberman, Reversible Object-Oriented Interpreters, Proceedings of the First European Conference on Object-Oriented Programming, Paris, Springer-Verlag, June 1987.
Lieberman 1989
Henry Lieberman, A Three-Dimensional Representation for Program Execution, IEEE Conference on Visual Languages, Rome, Italy, October 1989.
Lieberman 1990
Le Marcottage: Une Approche Navigationnelle de la Programmation par Objets, Rapport de Recherche 90-81, Laboratoire Informatique Théorique et Programmation, Université Paris 6, Octobre 1990.
Mittal, Bobrow and Kahn 1986
Sanjay Mittal, Daniel Bobrow and Kenneth Kahn, Virtual Copies: At the Boundary Between Classes and Instances, OOPSLA-86 ACM Conference on Object-Oriented Programming, Portland, Oregon, 1986.
Stallman 1984
Richard Stallman, Emacs: The Extensible, Customizable, Self-Documenting Display Editor, ACM Conference on Text Processing, 1984.
Stein, Lieberman, Ungar 1989
Lynn Stein, Henry Lieberman, David Ungar, The Treaty of Orlando: A Shared View of Sharing. In Object-Oriented Concepts, Applications and Databases, Won Kim and Fred Lochovsky, eds. Addison-Wesley 1989.
Travers 1989
Michael Travers, A Visual Representation for Knowledge Structures. ACM Conference on Hypertext, Pittsburgh, Pennsylvania, USA, October 1989.
Ungar and Smith 1986
David Ungar and Randall Smith, Self: The Power of Simplicity, OOPSLA-87 ACM Object-Oriented Programming Conference, Orlando, Florida, 1987.