Tiling a Square, Part 3
How many acute triangles do you need to cover the surface of a square?
It may be easier to consider the problem of tiling an obtuse
triangle. We know that any interior point has to have at least five
line segments connecting it, in order to satisfy the condition that
the angles are all less than 90 degrees. (In other words, it has to be
the interior point of a pentagon where there is a line segment going
to each of the vertices.) We also know that any vertices that are at
angles greater than 90 degrees must have at least one line segment
connected to it. We also know that every point on an edge has to have
at least two line segments connecting it. In the case of an obtuse
triangle, you need to divide the obtuse angle. This suggests the
introduction of a pentagon where one of the vertices is at the vertex
of the obtuse angle.

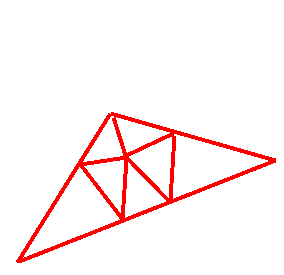
We could use the same reasoning and solve the problem for a square by
starting with the obtuse tiling solution:
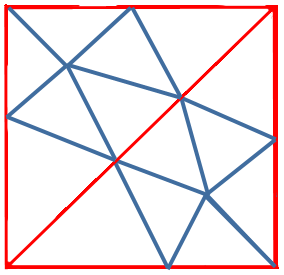
We do better by starting with the right tiling solution:
But we can do better still if we start in a corner of the square:
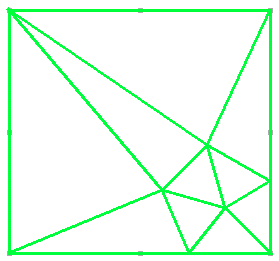
We need at least two interior points, hence two pentagons, but what if they
could overlap?
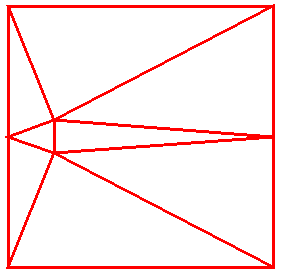
Note that any triangle (A) from the
corners to a point in the yellow region will be acute. Triangles (B)
are obtuse. Likewise, triangles (D) are acute and (C) are
obtuse. (Triangles with a vertex on the circle are right.)
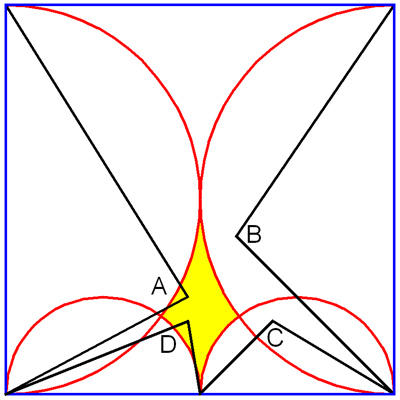
Martin Gardner found a
reference to this puzzle in a 1962 Austrialian Math Journal.
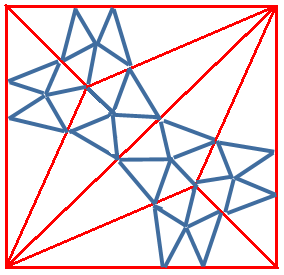
Other solutions:
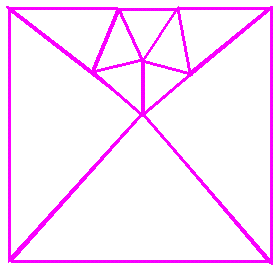
Recursive:
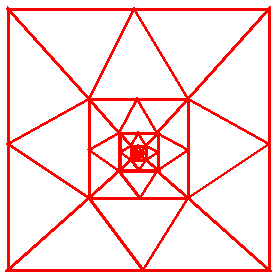
24:
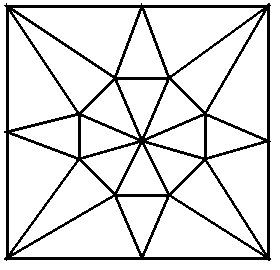
12:
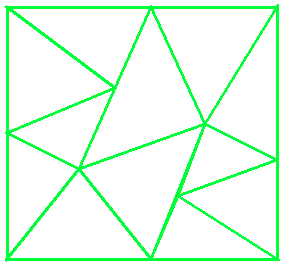
another way of doing just 10:
Tied Up In Knots
Can you pick up a string and tie a knot without letting go of either end?
Cross your arms before picking up the string.
Six cube

Oliver Selfridge asked me this puzzle:
Express the radius of
the circle in terms of a, b, and c.
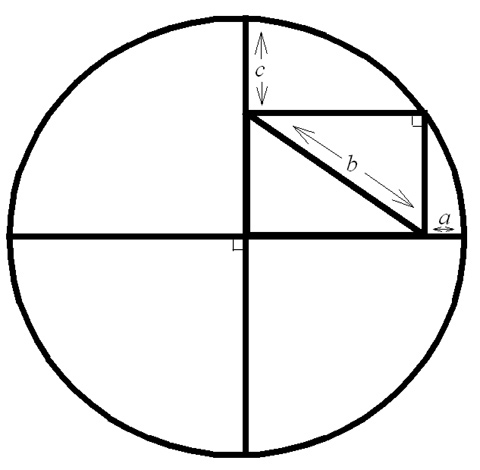
Oliver
says that Richard Feynman made the same mistake that you probably
made. The radius is equal to the length of the diagonal of the
rectangle, b.
Tonight's puzzles mostly deal with being pattern savvy.
Pennies From Heaven (or Hell)
By moving just three coins, make the triangle point down.

By making four slides, where a coin can only slide by rotating
around another until it comes to rest, turn the triangle into a
circle.

Arrange three coins in such a way that by flipping over two coins, three
times, you end up with all three heads up.

By moving just one coin, make two rows of four.

Arrange all five coins so that each one touches every other one.

Move four pennies to make five rows of four

Moving two adjacent pennies at a time, group heads with head and
tails with tails in just three moves, i.e., go from the top row
configuration to the bottom row configuration.

Pick-Up Sticks
Remove eight matches to leave just two squares.

Make four triangles, all this size, with just 6 matches.

Rearrange three matches to make eight equilateral triangles.

Move two matches to leave the olive outside of the glass.

Remove one match and rearrange to leave six equal shapes.
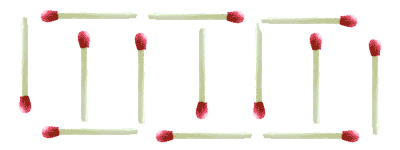
Remove six matches to leave ten.

Move two matches to leave seven squares.

Move four matches to leave six triangles.

Move four matches to leave three squares.

Remove six matches to leave two squares.

Remove three matches to leave three squares.

Move one match to make the house face east instead of west.

Rearrange to form seven diamonds.

Move two matches to leave four squares.

Move two matches to leave six squares.

Rearrange four matches to leave one.

This puzzler is inspired by the seventeenth century French engineer and mathematician, Gerard Desargues.
Using ten coins, make ten rows of three coins each.
Do the same thing with only nine coins.
Crossing the Moat
Use two matches to cross the moat:
Alternative version:
Rapunzel has a castle surrounded by a
rectangular moat that is ten feet across. She has two ten-foot boards
to use to cross the moat (which is more than 20 feet deep), but no
other materials or tools are available. In particular, the boards
cannot be nailed, glued or lashed together. How does she cross the
moat?