|
Numerical Mechanisms and Children’s Concept of Numbers
Natalia Marmasse,
Aggelos Bletsas,
Stefan Marti
Teachers try to convince their students that equations and formulas are more expressive than ordinary words. But it takes years to become proficient at using the language of mathematics, and until then, formulas and equations are in most respects even less trustworthy than commonsense reasoning. (Minsky in Society of Mind, p. 193, Mathematics Made Hard) To what extent is the sense of numbers innate, and to what extent is it learned? It seems that our brain, as well as those of other animals, is equipped from birth with a rudimentary number sense. Being able to perceive numbers in our surroundings has been significant to our survival, for example, in tracking predators or selecting the best foraging grounds. In animals, these mechanisms are limited mostly to small numbers. The mathematical level that humans have reached is by virtue of the fact that we have developed abilities for language and for symbolic representation. With these, we have developed representations for large numbers and algorithms for exact calculations. So arithmetic and number theories are built on our capacity for symbolic notation as well as our nonverbal ability to represent and understand numerical quantities. But what does innate, nonverbal, number sense exactly mean?
Numerosity and Ordinality of Infants Children, just like animals and adults, are quite accurate with very small numbers, and they can compute approximately with larger numbers. Piaget suggested that infants are born with no understanding of numerosity, which is the ability to discriminate arrays of objects on the basis of the quantity of items presented—for example, being aware of that a quantity of two is different than a quantity of three. Early Piaget experiments (Piaget 1942) described infants' lack of numerosity as a poor perception of quantity conservation. However, recent experiments have shown that infants between ages of 4 and 7 ½ months are able to discriminate two items from three items, but not 4 items from 6 items (Starkley et al. 1983). In particular, 7-month old infants were presented with two photographs of two or three items accompanied with two or three drumbeats. The infants looked longer at the photos with the number of items matching the number of drumbeats, indicating intuition of quantities up to 3 or 4 and suggesting at the same time that this ability for numerosity abstraction is neither visually nor auditory based (Geary 1994). Other experiments, conducted independently, showed that 10 to 12-month old infants could discriminate 3 from 4 items and, sometimes, 4 to 5 items (Strauss & Curtis 1981). Nevertheless, the experimental results mentioned above did not indicate that infants perceived that 2 is more than 1 or 3 is more than 2. That awareness of ordinal relationships between numerosities (ordinality) is developed slowly across small values (up to three or four) in the first 18 months of life (Geary 1994). At this age, infants are sensitive to small changes of small quantities, for example they seem to understand the result of addition 1+1=2 or subtraction 2-1=1. The ability to understand even small quantities (numerosity) from the first months of life therefore indicates that there is an innate mechanism for number sense which can provide the seed for further development of numerical skills and abilities.
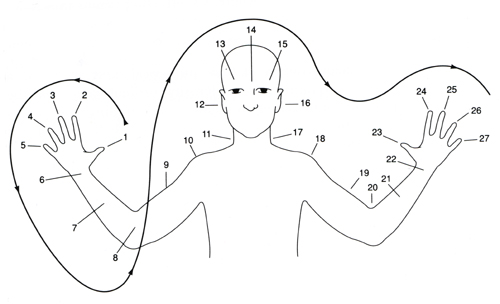
Numbers, Number Words and Counting The notions of numbers and counting dates back to prehistory, and all tribes or societies, however simple, have some system of counting. With the invention of writing, symbols were found to represent the numbers. Different methods of representing numeric symbols were invented, but the most common one was the division in groups of ten. The numeric systems invented vary across time and place, and there is no doubt that the properties of such a system can facilitate or impede the development of children’s mathematical understanding. Chinese (and Asian languages based on ancient Chinese) are organized such that the numerical names are compatible with the traditional 10-base numeration system. So spoken numbers correspond exactly to their written equivalent: 15 is spoken as "ten five" and 57 as "five ten seven." Most European systems of number words are irregular up to 100. For example in French, 92 is said as "four twenty twelve," corresponding to 4*20 + 12. The more complicated the number word system is, the harder it is for children to learn the counting sequence. An interesting system is that of the Oksapmin (Saxe 1982), a horticultural society in Papua New Guinea, where counting and numerical representations are mapped onto 27 body parts (Figure 1).
Figure 1: Oksapmin counting system, based on 27 body parts (Saxe 1982). Linguistic aspects of numeration systems not only can affect the speed of learning the counting sequence, but also influence the children’s understanding of base structure, place value (units, tens, etc.) and associated arithmetical computations. For example, Asian children have a better understanding of the 10-base concept than their first grade American peers. The system of spoken numbers affects the child’s cognitive representation of numbers. The speed at which numbers can be pronounced also has an affect on the child’s memory span for numbers. The ability to keep more number words in short-term memory seems to influence early mathematical skills which require counting, for example in problems of simple addition. Important is that children first learn number words ("one," "two," "three"…), and then couple them with their quantity concepts. How quickly those associations happen vary across different cultures as they are influenced by linguistic factors.
Counting Principles It should be emphasized that there is no reason to require a child to use conventional count words in the conventional order. It can be safely assumed that there is a need for a set of unique tags to tick off the items in a collection, during the counting process, using these tags in a fixed order. The set of number words meets these criteria, but then so do other sets of tags, like the alphabet. It is noteworthy that many languages have used the alphabet as count word tags, for example, Greek and Hebrew. Tags need not even be verbal. They may be idiosyncratic entities, including short-term memory bins (Gelman and Galistel 1978). In any case, independent of the kind of counting tags, whether they are number words, the alphabet or other child-dependent sequence, five principles govern and define counting. The first three deal with rules of procedure, or how to count; the fourth with the definition of countables or what to count and finally the fifth involves a composite of features of the other four principles. We will mention briefly the five counting principles that are based on the influential work of Gelman and Galistel (Gelman and Galistel 1978): The one-to-one principle This principle emphasizes the importance of assigning only one counting tag (number word, alphabet element, or other) to each counted object in the array. For example, the child should never state "one, two, two." To follow that principle, a child has to coordinate two processes, partitioning and tagging. This simply means that every item being counted needs to be transferred from the to-be-counted category o the counted category (partitioning) while a distinct tag must be set aside, not to be used again in the counting sequence (tagging). Children employ many strategies to facilitate the coordination of partitioning and tagging, pointing to the objects and stating at the same time the associated number word is a common one. The stable-order principle Counting involves more than the ability to assign arbitrary tags to the items in an array. The counting tags chosen must be arranged in stable (i.e. repeated) order. For example, the child might count three objects stating "one, three, four" and four objects by stating "one, three, four, five." The cardinal principle This principle reflects the child’s understanding that the last number word of an array of counted items has a special meaning: it represents the set as a whole and the numerosity of this set of items. It seems likely that the cardinal principle presupposes the one-to-one principle and the stable-order principle and therefore should develop after the child has some experience in selecting distinct tags and applying those tags in a set. The abstraction principle The realization of what is counted is reflected in this principle. A child should realize that counting could be applied to heterogeneous items like toys of different kinds, color, or shape and demonstrate skills of counting even actions or sounds! There are indications that many 2 or 3 year olds can count mixed sets of objects. The order-irrelevance principle The child has to learn that the order of enumeration (from left to write or right to left) is irrelevant. Consistent use of this principle does not seem to emerge until 4 or 5 years of age (German and Galistel 1978). Although children at the age of 3 seem to understand the basic principles of how to count, Piaget's experiments indicated that counting proficiency, and mature number sense do not emerge until the age of 8. It seems that the innate, primitive mechanism of number understanding and counting needs constant refinement through practice and experience. Minsky states that younger children possess adequate knowledge about amounts and numbers. However, they lack knowledge about their knowledge or "they have not acquired the checks and balances required to select or override their hordes of agents with different perceptions and priorities." (Minsky 1985).
Early Arithmetical Skills Starkey (1992) showed that very young children could represent numerical quantities without the use of language. Even more importantly, they could understand that addition increases the numerosity of the set of items, while subtraction does the opposite. Starkey used a box where a child could search for tennis balls without being able to look inside. Children were shown a small set of balls put into the box, and then asked to retrieve that set of balls. An assistant, in anticipation of every child’s retrieval, secretly put balls inside the search box so that their number remained constant. 36 to 42 month-old children were able to perceive numerosities of up to 4. When children were shown an additional placement or removal of 1 to 3 balls and then asked to search for the set of balls, the question was whether they would retrieve the number of balls placed originally, or whether they would search for the number of balls after the addition or subtraction. Nearly all 18-24 month-old children searched for the set of balls after the addition or removal, signifying that they could understand the result of a simple addition or subtraction of up to 4. The above experimental results do not contradict Piaget's experiments that suggest poor number sense and arithmetical efficiency of children until the age of 7: the Starkey experiments did not rely at all on visual cues—or, at least as much as Piaget’s! Moreover, the above experiment did show a deficiency for more complex addition and subtraction problems, at the preverbal stage of children life. Baroody and Ginsburg (1986) and others suggested that children adapt their already-existing counting skills and knowledge to problems requiring addition and subtraction. Adaptation occurs during the development of verbal counting, after children have learned the number words of their language and the strategies involved depend on each culture’s counting system. This remark is very important if we consider that children recognize and use counting as an addition/subtraction problem-solving strategy before formal education in school. Verbal counting seems to be a very reasonable arithmetical strategy, given that basic nonverbal skills of children appear to be applicable to only small values (Geary 1994).
Arithmetical Development As the child learns the culture’s number words and associates these words with sets of objects, for example, five with all of the fingers on one hand, the manipulation of quantities larger than those that the child can perceive innately becomes feasible. The basis for children arithmetical development seems to be formed initially through simple counting, using fingers or objects so that the child doesn’t lose track of what it has already counted. Later, after the child has gained some linguistic competence, verbal counting (thinking with number words) shapes the children's mathematical development. In early preschool years, object counting using manipulatives is common. Children solve simple addition and subtraction problems by counting the whole set (for the case of addition) or the remaining set (in the case of subtraction) of objects. Manipulatives can be our fingers or other body parts, like in the case of the Oksapmin. They help keeping track of what has already been counted and involve special techniques for problem solving. For example, a student can solve "10-3" by raising the fingers of the two hands, folding three and counting the rest. Verbal counting is a more mature technique, where the child uses neither fingers nor objects, but monitors the process using only short-term memory. For example, in order to solve "5+3," he can count mentally "5 6 7 8," and then, using the principle of cardinality, infer that the result is 8. Counting is an important exercise for children. It helps them explore the relationships between numbers. Reflecting on number ordinality and realizing that smaller numbers are included within bigger numbers helps them modify their problem solving strategies. For example, in order to solve "3+19," they should start counting from 19 and progress to "20 21 22" instead of starting from 3 and progressing to 19, because in the latter case, they would have to count much more, increasing the possibility of errors. This pattern of calculation therefore has its origins in the early counting explorations of every child. Because of its great importance and heavy use, the counting problem-solving strategy is an established, prominent skill even for adults. Skillful counting as well as gradual understanding of the numerical system improves children's number sense. The structure of the number words plays a significant role, as explained previously. Children with a better number sense are able to decompose numbers into smaller groups, usually around powers of 10 or 5, depending on the kind of the problem, or regroup them later, simplifying their problem solving strategies. Number regrouping and decomposition (derived facts) accelerate problem solving and improve number understanding. Practice and success in arithmetical operations form experience in terms of long term memory storage of basic facts about numbers. Thereinafter, the solution of simple arithmetical problems involves direct memory retrieval of "hard-wired" facts (or according to Minsky’s theory, K-lines): for example, to solve "5+3," the child after a certain age will answer directly 8 without having to count. It should be noted that children do not first solve simple numerical problems exclusively by means of finger counting, then exclusively through verbal counting, and finally through memory retrieval of facts about numbers, known from similar problems solved in the past. Rather, children have available to them a variety of all the above problem-solving strategies. As more arithmetical operations are performed, the available strategies are modified, some are complemented, some are abandoned, while some new ones are constructed from bits and pieces of existing procedures, depending on the new goals the child has set (goal-directed behavior). As the child gradually masters arithmetical operations, the variety of problem solving strategies changes, illustrating a shift from general reliance on finger/object counting, to verbal counting and finally, to more complex strategies like number-decomposition (for example, derived facts like 132 = 1x100 + 3x10 + 2x1) or memory retrieval based strategies. Again, it should be underlined that we are talking about a general shift, not a complete sacrifice of simple, primal problem-solving strategies (like finger counting) in favor of newer, more sophisticated ones (like direct memory retrieval).
Arithmetical Development and Education It is apparent that the child’s concept of numbers and arithmetic gradually changes, affecting the observable skills. The strongest influence on arithmetical development is formal education, which can lead to the development of skills that would not have emerged in a more natural environment, without formal instruction. We emphasize the importance of education in arithmetical (and therefore mathematical) development, as it is claimed by recent neuropsychology research that "every human being is endowed with a primal number sense, an intuition about numerical relations. Whatever is different in adult brains is the result of successful education, strategies, and memorization"(Dehaene 1997). However, if formal education is so important for arithmetical-mathematical development and achievement, why do so many schoolchildren fear mathematics? Numbers and arithmetic (and therefore mathematics) are part of our everyday life, but why do they seem de-contextual from commonsense and human life when they are taught in classrooms? Moreover, how can modes of teaching affect ways of thinking about numbers? How can different teaching approaches improve children’s arithmetical problem solving strategies? Traditional approach Traditional arithmetic curricula focus on the acquisition of basic numerical skills such as number order and counting, addition and subtraction facts, place value, as well as algorithms and procedures for complex addition and subtraction. Emphasis is placed on the dissemination of formal definitions, easily understood by the students who are viewed as "blank slates" onto which information is etched by the teacher, in a didactic manner (Goodrow 1998). The character of that information is mainly procedural knowledge about standard algorithms and methods for arithmetic problem solving. With this "authoritative" pedagogy of arithmetic, children ought to start thinking in a certain way in order to solve numerical problems. Therefore, students might be forced to change their own way of thinking. We think that this approach restricts the variety of useful representations for mathematical thinking. We also hypothesize that the procedural knowledge, taught at traditional schools in the form of "ready to use" methods and algorithms, narrows down children's mental strategies for problem solving. Constructivism approach There is strong evidence that the early teaching of standard procedures for arithmetic problem solving "thoroughly distorts in children’s mind the fact that mathematics is primarily reasoning." (Kamii et al.1993). In order to address the above problem, new mathematics curricula have been introduced, based on the Piaget theory of Constructivism. This approach suggests that logico-mathematical knowledge, apart from empirical or social knowledge (Novick 1996), is a kind of knowledge that each child must create from within, in interaction with the environment, rather than acquire it directly (almost "being donated") from the environment. Students are viewed as thinkers with emerging theories about the world while teachers generally refrain from teaching procedures and algorithms but instead, behave in an interactive way with the students, encouraging them to invent their own methodologies for all four arithmetical operations (Goodrow 1998). Examples and evaluation of the two approaches Experimental research showed that students in classes using the constructivist approach developed better number sense and at the same time came up with several different representations of arithmetic values and expressions, leading to significantly better performance on numerical operations, compared to their age-mates from "traditional" classes. For example, constructivist students were able to represent the same number with several terms and more than one operation (i.e. 150 = 50x3 = 70+60+20 = 500-400+50) while traditional (non-constructivist) students used only two terms and one operation (12 = 6+6 = 5+7 = 4+8). Performance on 2-digit addition was more or less the same between students of the two groups, however, on 2-digit subtraction and especially in cases with place values, the performance of constructivist students was much better. They could use several different ways to decompose and regroup the numbers, having an excellent number sense, while their non-constructivist age-mates were using the traditional, column-wise from right to left algorithm, making, in a lot of cases, several mistakes with the place value, indicating a poor sense of numbers. For example, for the simple calculation 28-9, a non-constructivist second-grade student replied:
One constructivist second-grade student approach was:
Another constructivist approach was:
The last approach is amazing since it involves calculations with negative numbers, which are a difficult notion for second-grade elementary school students. Traditional students would not be able to perform such reasoning, probably because they are not familiar yet with algebra of negative numbers. Generally, children perform much better using their own ways of thinking rather than standard, taught procedures. The majority of errors among the non-constructivist students are mainly caused because of a lack of number sense and a poor generalization of the standard procedures on unknown problems. That is very natural and can be nicely explained by Minsky’s theory: "Formal definitions lead to meaning networks as sparse and thin as possible." The useful "meanings" are not the flimsy chains of definition but the much harder-to-express networks of ways to remember, compare, and change things. "A logic chain can break easily, but you get stuck less often when you use a web of cross-connected meaning-network." It should be noted that we are talking about the constructivist approach applied to early classes of elementary school, mainly first and second grade. At this level, the main goal is for children to accumulate a good number sense and practice many different kinds of reasoning (Papert’s Principle). Nevertheless, we believe that a more balanced approach between conceptual knowledge and procedural knowledge should be followed at the next elementary school levels. New algorithms and numerical techniques taught in later classes of elementary school can be built on top of well established, early developed skills like strong number sense. Most likely such a combination of educational approaches would make children expand their numerical and mathematical abilities, without them being reluctant to tamper with their old, tested problem solving strategies (Investment’s Principle).
To answer our initial question, whether number sense is innate or learned: It should be clear by now that both elements, nature as well as nurture, influence a persons early arithmetic reasoning skills. Mathematical reasoning is neither innate nor learned, but most likely a combination of both. Finally, it should be emphasized that education and educational models are coupled with every society’s culture. Unfortunately, if a versatile and multidimensional arithmetical and mathematical education model stands orthogonal to the prominent cultural ideal, for example, that children’s idols are basketball or football stars, then any educational model proposed, be it constructivist or not, is doomed to fail.
Applet In the applet, we demonstrate basic arithmetical problem-solving strategies, like the ones described above. The explanations that are part of the output depend both on the educational model and the kind of problem that has to be solved. References Baroody, A.J. & Ginsburg, H.P. (1986). The Relationship between Initial Meaningful and Mechanical Knowledge of Arithmetic. In J. Hiebert (Ed.) Conceptual and Procedural Knowledge: The Case of Mathematics, pp. 75-112. Hillsdale, N.J.: Lawrence Erlbaum Associates. Dehaene, S. (1997). What Are Numbers, Really? A Cerebral Basis For Number Sense (EDGE 28 — October 27, 1997) [WWW document]. URL http://www.edge.org/3rd_culture/dehaene/dehaene_p2.html (visited 2000, May 11).Geary, D.C. (1994). Children’s Mathematical Development: Research and Practical Applications. Washington, DC: American Psychological Association. Gelman R. & Gallistel C.R. (1978). The Child’s Understanding of Number. Cambridge, MA: Harvard University Press. Goodrow, A.M. (1998) Modes of Teaching and Ways of Thinking. Paper presented at the International Society for the Study of Behavioral Development, Bern, Switzerland, July 1998. (Summary of: Children's Construction of Number Sense in Traditional Constructivist, and Mixed Classrooms. Unpublished dissertation for the degree of Doctor of Philosophy in Child Development. Medford, MA: Tufts University, May 1998). Available online at URL http://www.terc.edu/investigations/eval/html/eval-2.goodrow.html (visited 2000, May 11).Kamii, C., Lewis B. A., Livingston S. J. (1993). Children Inventing Their Own Procedures. Arithmetic Teacher, 12/1993. Available online at URL http://www.enc.org/reform/journals/104005/4005.htm (visited 2000, May 11).Minsky, M. (1985). The Society of Mind. New York, NY: Simon & Schuster. Novick, R. (1996). Developmentally Appropriate and Culturally Responsive Education: Theory in Practice. Portland, OR: Northwest Regional Educational Laboratory. Available online at URL http://www.nwrel.org/cfc/publications/dap2.html (visited 2000, May 11).Piaget, J. (1942). The child’s conception of number. London: Routledge & Kegan Paul. Saxe, G. B. (1982). The development of measurement operations among the Oksapmin of Papua New Guinea. Child Development, 53, 1242-1248. Available online at URL http://www-gse.berkeley.edu/faculty/gsaxe/oksapmin/oksapmin.html (visited 2000, May 11).Starkey, P. (1992). The Early Development of Numerical Reasoning. Cognition 43, 93-126. Starkey P., Spelke E.S., Gelman R. (1983). Detection of Intermodal Numerical Correspondences by Human Infants. Science 222, 179-181. Strauss M.S., Curtis L.E. (1981). Infant Perception of Numerocity. Child Development 52, 1146-1152. Version 6, May 11th, 2000 |