Projections and Projection Matrices
Nov 27, 2015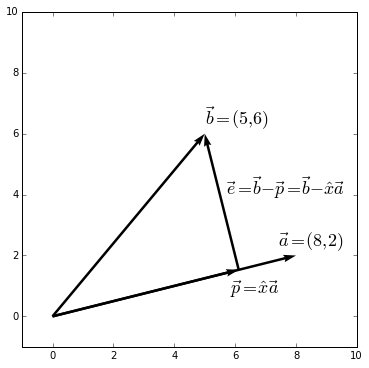 As a simple example we project on to a line. First, calculate \(e\) and \(p\).
As a simple example we project on to a line. First, calculate \(e\) and \(p\).
\[\begin{align} 0 &= \vec{e} \bullet{}\vec{a} && \vec{e} \perp \vec{a} \text{ so the dot product is zero}\\ 0 &= (\vec{b}-\hat{x}\vec{a})\bullet{}\vec{a} && \text{notice } \vec{e} = \vec{b}-\vec{p} = \vec{b}-\hat{x}\vec{a}\\ 0 &= \vec{b}\bullet \vec{a} - \vec{a} \hat{x}\bullet \vec{a} && \text{distribute } \vec{a}\\ 0 &= (\vec{b} \bullet \vec{a}) - \hat{x} (\vec{a} \bullet \vec{a}) && \text{notice } \hat{x} \text{ is a scalar, so the last term can be } \hat{x} \vec{a} \bullet \vec{a}\\ \hat{x} (\vec{a} \bullet \vec{a}) &= (\vec{b} \bullet \vec{a})\\ \hat{x} &= \dfrac{\vec{b} \bullet \vec{a}}{\vec{a} \bullet \vec{a}} \implies \vec{p} = \dfrac{\vec{b} \bullet \vec{a}}{\vec{a} \bullet \vec{a}} \vec{a} && \text{because } \vec{p} = \hat{x}\vec{a} \end{align}\]
We can summarize the projection to the matrix as, \(\vec{p} = P\vec{b}\). This is easy to find if we present the equation the other way around. Notice that with vectors the order is inconsequential, because \(\vec{a} \bullet \vec{b} = \vec{b} \bullet \vec{a}\)
\[\begin{align} 0 &= \vec{a} \bullet \vec{e} && \vec{a}, \vec{e} \text{ on opposite sides}\\ 0 &= (\vec{a} \bullet \vec{b}) - \hat{x}(\vec{a} \bullet \vec{a})\\ \hat{x}(\vec{a} \bullet \vec{a}) &= (\vec{a} \bullet \vec{b})\\ \hat{x} &= \dfrac{\vec{a} \bullet \vec{b}}{\vec{a} \bullet \vec{b}} = \dfrac{\vec{a}^T\vec{b}}{\vec{a}^T\vec{a}} \end{align}\]
With \(\hat{x}\) in this form, we can calculate the permutation matrix, \(P\) from \(\vec{p} = P\vec{b}\)
\[\begin{align} \vec{p} &= \vec{a}\dfrac{\vec{a}^T\vec{b}}{\vec{a}^T\vec{a}}\\ \vec{p} &= \dfrac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}}\vec{b} \implies P = \dfrac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}} && \text{because } \vec{p}= P\vec{b} \end{align}\]
Project Onto a Plane in \(\mathbb{R}^3\)
Note that \(\vec{a}^T\vec{a}\) in the denominator evaluates to a scalar. If we want to project onto a plane, the denominator becomes \(A^TA\), which evaluates to a matrix.
- Division by a matrix has no meaning. You cannot divide by a martix.
- In arithmatic, we undo multiplication with division.
- To undo the effects of a matrix multiplication, we multiply the inverse of the matrix. \(A^{-1}A\vec{b}=\vec{b}\)
- We must re-arrange the equation so that we use inverse matrices instead of division.
We can think of projecting onto a plane as projecting onto multiple vectors. To project \(\vec{b}\) onto \(A\), we are looking for the vector \(\hat{x}\), such that \(\vec{p}=A\hat{x}\), where \(\vec{p}\) is the point on the plane closest to \(\vec{b}\). The first step is to find the vector \(\hat{x}\).
Like the first example, we define the error vector, \(\vec{e}\), as the vector that goes from the plane to \(\vec{b}\)
\[\begin{equation*} \vec{e} = \vec{b} - A\hat{x} \end{equation*}\]
Assume \(A\) is a matrix made of two vectors, \(a_1\) and \(a_2\) in \(\mathbb{R}^3\):
\[\begin{equation} A = \begin{bmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \\ a_{13} & a_{23} \end{bmatrix} \end{equation}\]
Our error vector, \(\vec{e}\) will be perpendicular to both \(a_1\) and \(a_2\). We want to find the closest point on \(A\) to \(\vec{b}\). Set \(\vec{e}\) and \(\vec{a}\) perpendicular \(0 = \vec{a}_n^T\vec{e}\)
\[\begin{align} 0 &= \vec{a}_1^T(\vec{b} - A\hat{x})\\ 0 &= \vec{a}_2^T(\vec{b} - A\hat{x}) \end{align}\]
There is a simple way to write the equation that captures all components at once.
\(A^T(\vec{b}-A\hat{x})\)
Which can be written as
\(A^T\vec{b} = A^TA\hat{x}\)
Which can be solved for \(\hat{x}\)
\((A^TA)^{-1}A^T\vec{b} = \hat{x}\)
Now that we have the \(\hat{x}\) vector, we can find the projection matrix. Remeber that \(\vec{p} = P\vec{b}\). If we can arrange the equation above correctly, it gives us \(P\).
\(\vec{p} = A\hat{x}\)
Subsitute \(\hat{x}\)
\(\vec{p} = A(A^TA)^{-1}A^T\vec{b}\)
Now the equation is in the form \(\vec{p} = P\vec{b}\), so
\(P = A(A^TA)^{-1}A^T\)